L'énoncé
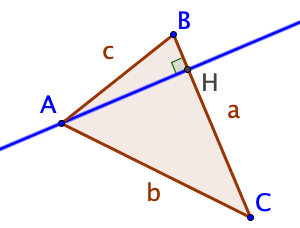
On utilise la figure suivante : avec $(AH)$ la hauteur issue du sommet $A$.
Cocher la bonne réponse
Tu as obtenu le score de
Question 1
Quelle est la formule usuelle de l'aire d'un triangle ?
$\dfrac{AH\times BC}{2}$
$\dfrac{AB\times BC}{2}$
$\dfrac{AH\times AC}{2}$
$\dfrac{AB\times AC}{2}$
La formule est $\dfrac{base\times hauteur}{2}$ c'est donc $\dfrac{AH\times BC}{2}$.
Question 2
Quelle formule peut-on en déduire pour l'aire d'un triangle ?
$\dfrac{ac\times \sin(\widehat{C})}{2}$
$\dfrac{bc\times \sin(\widehat{C})}{2}$
$\dfrac{ab\times \sin(\widehat{C})}{2}$
$\dfrac{ac\times \sin(\widehat{A})}{2}$
On part de la formule usuelle et on fait la même démonstration que dans la vidéo de cours.
Question 3
Que vaut la hauteur $AH$ ?
$\sin(\widehat{C})\times c$
$\sin(\widehat{B})\times a$
$\sin(\widehat{C})\times b$
On applique la formule du sinus d'un angle dans le triangle rectangle $AHC$ rectangle en $H$ :
$\sin(\widehat{C})=\dfrac{AH}{AC}$ puis on effectue un produit en croix :
$AH=\sin(\widehat{C})\times b$
Question 4
L'aire est donnée par : $\dfrac{ab\times \sin(\widehat{C})}{2}$
Application numérique : on prend a=3 cm, b=5 cm et l'angle $\widehat{C}=30°$
Que vaut l'aire du triangle $ABC$ ?
$4,25 cm^2$
$3,25 cm^2$
$4,75 cm^2$
$3,75 cm^2$
On utilise la formule Aire=$\dfrac{ab\times \sin(\widehat{C})}{2}$ et on obtient donc
Aire =$\dfrac{3\times 5\times \sin(30)}{2}= 3,75$ $cm^2$.
Question 5
Que vaut alors la hauteur $AH$ sachant que l'aire de $ABC$ vaut $3,75 cm^2$ ?
On reprend les mêmes applications numériques : a=3 cm, b=5 cm et l'angle $\widehat{C}=30°$.
2 cm
2,5 cm
3 cm
3,5 cm
L'aire valait 3,75$cm^2$ et la formule usuelle est Aire=$\dfrac{AH\times BC}{2}$
On a donc $AH =\dfrac{2\times aire}{a}=2,5 cm$
Question 6
Application numérique : on prend c=5 cm, b=9 cm et l'angle $\widehat{A}=45°$
Que vaut l'aire du triangle $ABC$ ?
$15cm^2$
$15,86cm^2$
$16cm^2$
$16,86cm^2$
On utilise la formule en l'adaptant Aire=$\dfrac{cb\times \sin(\widehat{A})}{2}$ et on obtient donc :
Aire=$\dfrac{9\times 5\times \sin(45)}{2}$ qui vaut 15,85$cm^2$.
Question 7
On note $H'$ la hauteur issue de $B$. Que vaut alors la hauteur $BH'$ ?
On reprend les mêmes applications numériques : $c=5 $cm, $b=9 $cm et l'angle $\widehat{A}=45°$.
L'aire valait $15,86$ $cm^2$.
3,5 cm
3 cm
4 cm
3,75 cm
L'aire valait 21,27$cm^2$ et la formule usuelle est Aire=$\dfrac{BH'\times AC}{2}$
On a donc $AH' =\dfrac{2\times aire}{b}=3,5 cm$
Question 8
Application numérique : on prend a=4 cm, c=6 cm et l'angle $\widehat{B}=60°$
Que vaut l'aire du triangle $ABC$ ?
8,76$cm^2$
8,6$cm^2$
8,58$cm^2$
8,66$cm^2$
On utilise la formule en l'adaptant Aire=$\dfrac{ca\times \sin(\widehat{B})}{2}$ et on obtient donc :
Aire=$\dfrac{4\times 6\times \sin(60)}{2}$ qui vaut environ 8,58$cm^2$.
Question 9
On note $H''$ la hauteur issue de $C$. Que vaut alors la hauteur $CH''$ ?
On reprend les mêmes applications numériques : a=4 cm, c=6 cm et l'angle $\widehat{B}=60°$.
L'aire valait 8,58$cm^2$.
5,12 cm
5,44 cm
6,12 cm
6,44 cm
L'aire valait 8,58$cm^2$ et la formule usuelle est Aire=$\dfrac{CH''\times AB}{2}$
On a donc $AH'' =\dfrac{2\times aire}{C}=6,12 cm$
Question 10
Application numérique : on prend a=15 cm, b=12 cm et l'angle $\widehat{C}=30°$
Que vaut l'aire du triangle $ABC$ ?
35$cm^2$
40$cm^2$
45$cm^2$
50$cm^2$
On utilise la formule Aire=$\dfrac{ab\times \sin(\widehat{C})}{2}$ et on obtient donc :
Aire=$\dfrac{12\times 15\times \sin(30)}{2}$ qui vaut 45$cm^2$.
