L'énoncé
Cocher la bonne réponse. Les valeurs seront arrondies au centième.
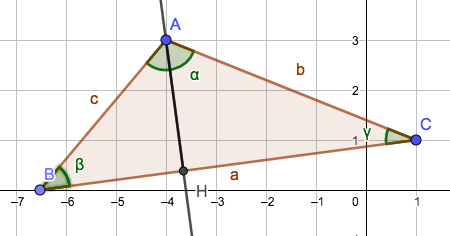
On utilisera le triangle $ABC$ suivant.
Tu as obtenu le score de
Question 1
On sait que $a=5,3$ cm, $b=4,$5 cm et $AH$ la hauteur issue du sommet $A$ vaut $4,2$ cm.
Que vaut $sin(\gamma)$ ?
$0,93$
$0,47$
$0,62$
$0,84$
On calcule l'aire avec la formule usuelle avec la hauteur.
Après on utilise la formule de l'aire avec le sinus.
La formule usuelle de l'aire avec la hauteur donne $aire =\dfrac{base\times hauteur}{2}$ soit ici $\dfrac{a\times AH}{2}$.
On a donc $aire =11,13 cm^2$.
On sait de plus que $aire=\dfrac{a\times b\times \sin(\gamma)}{2}$
On a donc $\sin(\gamma)=\dfrac{2\times aire}{a\times b}$
Et $\sin(\gamma)= 0,93$
Question 2
On sait que $c=6,8$ cm, $b=9,3$ cm et $BH$ la hauteur issue du sommet $B$ vaut $3,1$ cm.
Que vaut $\sin(\alpha)$ ?
$0,74$
$0,45$
$0,52$
$0,81$
Calculer l'aire avec la formule usuelle.
Utiliser la formule de l'aire avec le sinus.
La formule usuelle de l'aire avec la hauteur donne
$aire =\dfrac{base\times hauteur}{2}$ soit ici $\dfrac{b\times BH}{2}$.
On a donc $aire =14,415 cm^2$.
On sait de plus que $aire=\dfrac{c\times b\times \sin(\alpha)}{2}$
On a donc $\sin(\alpha)=\dfrac{2\times aire}{c\times b}$
Et $\sin(\gamma)= 0,45$
Question 3
On sait que $a=4,6$ cm, $c=8,1$ cm et $CH$ la hauteur issue du sommet $C$ vaut $2,1$ cm.
Que vaut $\sin(\beta)$ ?
$ 0,58$
$ 0,69$
$ 0,46$
$ 0,93$
Mêmes astuces que précédemment.
La formule usuelle de l'aire avec la hauteur donne
$aire =\dfrac{base\times hauteur}{2}$ soit ici $\dfrac{c\times CH}{2}$.
On a donc $aire =8,505 cm^2$.
On sait de plus que $aire=\dfrac{c\times a\times \sin(\beta)}{2}$
On a donc $\sin(\beta)=\dfrac{2\times aire}{c\times a}$
Et $\sin(\beta)= 0,46$
Question 4
On sait que $b=3,2$cm, $c=6,$4 cm, $\sin(\alpha)=23°$ et $AH = 1,3$ cm.
Quelle est l'aire du triangle $ABC$ ?
$3,3 cm^2$
$3,6 cm^2$
$5,6 cm^2$
$4 cm^2$
Utiliser la formule du sinus plus que celle avec la hauteur.
On doit utiliser la formule avec le sinus et on trouve et on $aire =4 cm^2$.
Question 5
On reprend les mêmes données que précédemment : $b=3,2$cm, $c=6,4$ cm, $\sin(\alpha)=23°$ et $AH = 1,3$ cm et on admet que l'aire vaut 4$cm^2$.
Que vaut la longueur $a$ ?
$4,62$
$6,15$
$7,93$
$3,71$
On utilise la formule de l'aire avec la hauteur $aire= \dfrac{a\times AH}{2}$
On a donc $a=\dfrac{2 \times aire}{AH}$ qui donne $6,15$ cm.
