L'énoncé
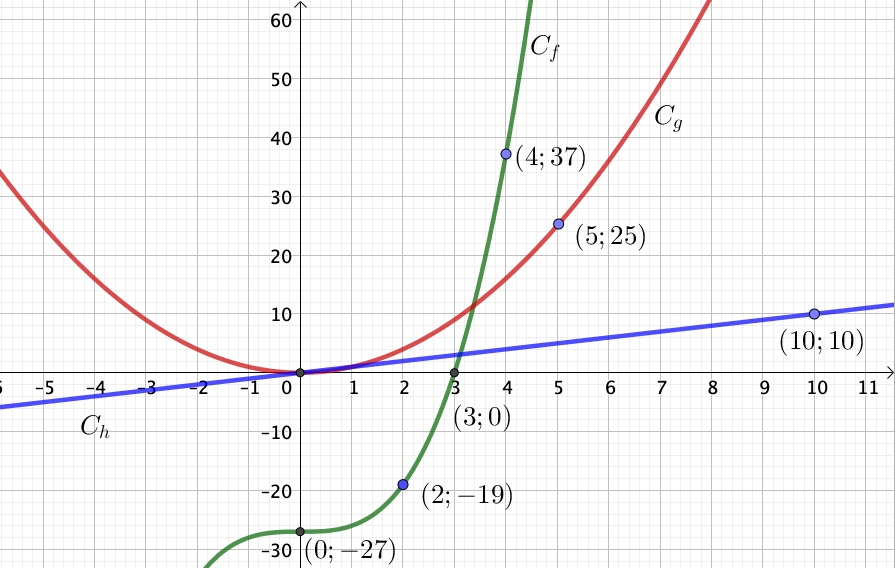
Soit les fonctions $f,h$ et $g$ dont les représentations graphiques sont respectivement $C_f,C_h,C_g$.
Question 1
Déterminer graphiquement les antécédents des nombres $0$ ; $-19$ et $37$ par la fonction $f$.
Le nombre $0$ à pour antécédent $3$.
Le nombre $-19$ à pour antécédent $2$.
Le nombre $37$ à pour antécédent $4$.
L'antécédent d'un nombre $p$ par la fonction $f$ est $x$ tel que $f(x)=p$.
Question 2
Déterminer les expressions analytiques des fonctions $f,g$ et $h$h
$f(x)=x^3-k$
$g(x)=Cx^2$
$h(x)=ax+b$ avec $k, a,b$ et $C$ réels que l'on déterminera :
On reconnait que $C_h$ est la représentation de la fonction $h(x)=x$. En effet, elle passe par l'origine et par le point $(10;10)$
La représentation $C_g$ est celle de la fonction $f(x)=x^2$. En effet, elle ^passe par l'origine et par le point $(5;25)$
On reconnait enfin la forme de la fonction cube dans le tracé $C_f$ qui passe par le point ($0;-27)$ donc $f(x)=x^3-27$.
Se ramener au tracé de la fonction cube.
Question 3
Déterminer graphiquement la valeur approchée de $x$ telle que $f(x)=h(x)$.
Par lecture graphique on obtient environ $x=3.2$ avec la précision de la figure.
Chercher le point d'intersection des deux courbes associées.
Question 4
Faire de même entre les fonctions $f$ et $g$.
On obtient la valeur $x=3.4$ avec la précision de la figure.
Question 5
Donner grâce au graphique et la question précédente le tableau de signe de la fonction $j(x)=x^3-x^2-27$.
On admettra que $f(x)=g(x)$ pour $x=3.4$
On note que$j(x)=f(x)-g(x)$.
Ainsi, lorsque $C_f$ est au dessous de $C_g$, cela signifie que $f(x)\leq g(x) \iff f(x)-g(x)\leq0\iff j(x)\leq0$
Le tableau de signe est le suivant :
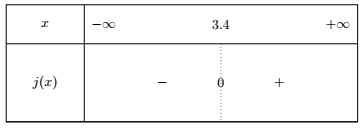
Reconnaître que $j(x)=f(x)-g(x)$.
