Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
La fonction cube
Définition
Soit $f$ la fonction cube définie pour tout $x \in \mathbb{R}$ par $f(x) = x^3$.
Exemples
Calculons quelques valeurs de la fonction.
$f(0) = 0^3 = 0 \times 0 \times 0 = 0$.
$f(-2) = (-2)^3 = (-2) \times (-2) \times (-2) = 4 \times (-2) = -8$.
$f \left (\dfrac{2}{3} \right ) = \left (\dfrac{2}{3} \right ) ^3 = \dfrac{8}{27}$.
Signe et variations
$f$ est négative lorsque $x$ est négatif et positive lorsque $x$ est positif.
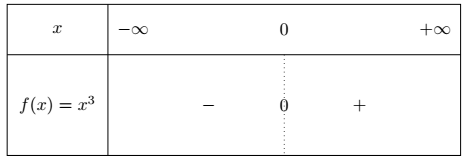
Tableau de variation :
La fonction cube est croissante.
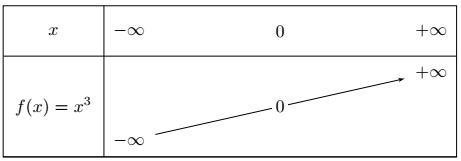
La courbe de la fonction cube est la suivante.
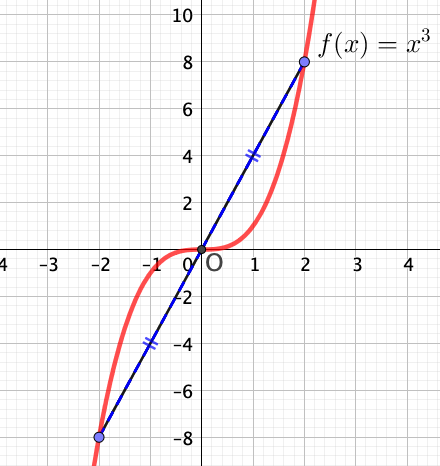
Propriétés
Soit $x \in \mathbb{R}$,
on calcule l'image de l'opposé de $x$:
$f(-x) = (-x)^3 = (-x) \times (-x) \times (-x) = x^2 \times (-x) = - x^3 = -f(x)$.
Ainsi $f(-x) = -
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
