L'énoncé
Exercice : équations de droites dans un triangle.
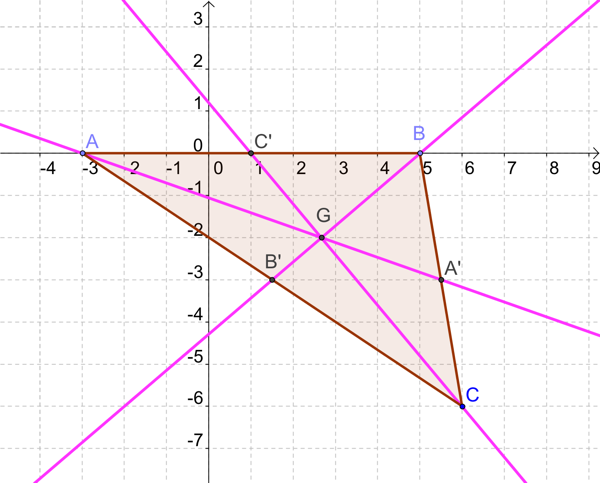
Dans un plan muni d'un repère orthonormé, on considère un triangle \(ABC\) avec \(A(-3 ; 0)\), \(B(5 ; 0)\) et \(C(6 ; -6)\).
On note \(A'\), \(B'\) et \(C'\) les milieux respectifs des côtés \([BC]\), \([AC]\) et \([AB]\).
Question 1
Calculez les coordonnées des points \(A'\), \(B'\) et \(C'\).
Pour \(A\), on a :
\( \left\{ \begin{array}{rcl} x_{A'} = \dfrac{x_B + x_C}{2} \\ y_{A'} = \dfrac{y_B+y_C}{2} \end{array}\right. \) soit \( \left\{ \begin{array}{rcl} x_{A'} = \dfrac{5+6}{2} \\ y_{A'} = \dfrac{0-6}{2} \end{array}\right. \)
Finalement : \(A'(5,5 ; -3) \)
Pour les mêmes raisons, on trouve : \(B'(1,5 ; -3) ; C'(1 ; 0)\).
Faites une figure.
Connaissez-vous les formules pour trouver les coordonnées du milieu d’un segment ? Voir la vidéo dans les pré-requis.
Question 2
Déterminez une équation de la droite \((AA')\), de la droite \((BB')\) et de la droite \((CC')\).
Concernant la droite \((AA)\) :
Notons \(m_1\) son coefficient directeur.
On a :
\(m_1 = \dfrac{-3-0}{5.5-(-3)}\)
\(m_1 =\dfrac{-3}{8.5} =-\dfrac{6}{17}\).
Une équation de la droite \((AA)\) est donc de la forme : \(y = \dfrac{-6}{17}x + b\).
Remplaçons les coordonnées de \(A\) dans l'équation, il vient :
\(0 = \dfrac{-6}{17} \times (-3) +b\)
Soit \(b = -\dfrac{18}{17}\)
Conclusion : l'équation de la droite \((AA)\) est : \(y = \dfrac{-6}{17}x -\dfrac{18}{17}\).
Pour les mêmes raisons, une équation de \((BB')\) est : \(y = \dfrac{6}{7}x -\dfrac{30}{7}\).
Et une équation de \((CC')\) est : \(y = -\dfrac{6}{5}x + \dfrac{6}{5}\).
Savez-vous calculer le coefficient directeur d’une droite sécante à l’axe des ordonnées dont on connait les coordonnées de deux points ? Voir la vidéo dans les pré-requis.
Une fois qu’on connait le coefficient directeur, on remplace les coordonnées d’un des deux points dans l’équation.
On trouve ainsi l’ordonnée à l’origine et le travail est terminé.
Question 3
Calculez les coordonnées du point d'intersection \(G\) des droites \((AA')\) et \((BB')\).
Résolvons : \( \left\{ \begin{array}{rcl} y = - \dfrac{6}{17}x - \dfrac{18}{17} \\ y = \dfrac{6}{7}x - \dfrac{30}{7} \end{array}\right. \)
Les deux membres de droite des deux égalités sont égaux donc on a :
\(\dfrac{-6x}{17} - \dfrac{18}{17} = \dfrac{6x}{7} + \dfrac{-30}{7}\)
Le dénominateur commun est \(17 \times 7\) soit 119. Ainsi :
\(102x+42x=-126+510\)
\(144x=384\)
On simplifie par 48 et \(x = \dfrac{8}{3}\). Remplaçons cette valeur dans la seconde ligne par exemple.
Ainsi : \(y = \dfrac{6}{7} \times \dfrac{8}{3}-\dfrac{30}{7}\)
\(y = \dfrac{48}{21}-\dfrac{90}{21}\)
\(y= -2\)
Conclusion : \(G\) a pour coordonnées : \(G(\dfrac{8}{3} ; -2)\)
Les coordonnées du point \(G\) vérifient les équations de \((AA')\) et \((BB')\) donc sont solutions du système.
Un point est à l’intersection de deux droites s’il est à la fois sur l’une et sur l’autre.
En mathématiques, on traduit le ET par une accolade.
On résout donc un système de deux équations à deux inconnues.
Les deux équations sont bien sur les équations réduites de \((AA’)\) et de \((BB’)\).
Question 4
Le point \(G\) est-il sur la droite \((CC')\) ?
1ère méthode : \(G\) est l'intersection de \((AA')\) et \((BB')\) qui sont deux médianes du triangle \(ABC\).
Donc \(G\) est le centre de gravité du triangle et \((CC')\) la troisième médiane donc \(G\) appartient à \((CC')\).
2ème méthode : \(6 \times \dfrac{8}{3}+5 \times (-2)-6 = 16 - 10-6 = 0\)
Les coordonnées de \(G\) vérifient l'équation de \((CC')\) donc \(G\) appartient à la droite \((CC')\).
C’est le moment de vous demander ce que représente le point \(G\) pour le triangle.
Sinon, vous pouvez remplacer les coordonnées de \(G\) dans l’équation de \((CC’)\) mais c’est moins élégant.
Question 5
L'équation \(x - y + 4 = 0\) est-elle une équation de \((AC')\) ?
Les coordonnées de \(A\) et \(C'\) sont-elles solutions de l'équation \(x-y+4 = 0\) ?
\(-3-0+4 = 1\)) donc \(A\) n'appartient pas à cette droite et \(x-y+4 = 0\) n'est pas une équation de la droite \((AC')\).
Pour que ce soit une équation de \((AC’)\), il faut bien sur que \(A\) et \(C’\) soient sur cette droite.
Testez donc leur appartenance en remplaçant leurs coordonnées dans l’équation.
