Fiche de cours
Équations de droites
Définition:
On se place dans le plan muni d'un repère.
Toute droite du plan possède une équation de la forme :
$x = k$ si il s'agit d'une droite parallèle à $(Oy)$, où $k$ est un réel
$y = ax + b$ si il s'agit d'une droite sécante à $(Oy)$ : c'est l'équation réduite de la droite.
$a$ est un réel correspondant au coefficient directeur de la droite, il donne l'inclinaison de la droite.
$b$ est un réel correspondant à l'ordonnée à l'origine, c'est à dire l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées.
Exemple :
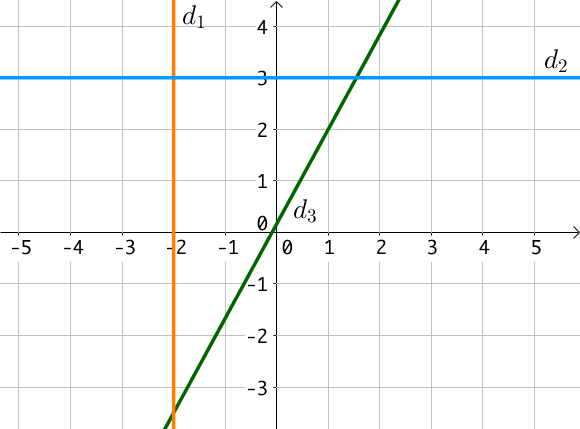
La droite $(d_1)$ est parallèle à l'axe des ordonnées. Son équation est donc de la forme $x = k$. Ainsi $k$ correspond à la valeur de l'abscisse. Tous les points de la droite ont même abscisse : $-2$, alors que leurs ordonnées sont variables. Ainsi, $x = -2$.
Un point quelconque
