L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
On considère la droite \(D\) d'équation : \(2x-4y = 6\)
Son coefficient directeur est :
-2
2
\(\dfrac{1}{2}\)
Aucune des trois réponses précédentes n’est exacte.
Il faut écrire cette équation sous la forme \(y = mx+p\).
Pour cela, isolez le terme en y dans le membre de gauche et divisez par -4.
Le coefficient directeur est d’après votre cours le nombre…
…\(m\) bien sûr. Le nombre \(p\) est l’ordonnée à l’origine.
Question 2
On considère la droite \(d\) d'équation \(x = 5\) et la droite \(d'\) d'équation \(y = 5\).
Les droites sont parallèles.
Les droites se coupent au point de coordonnées \((-5 ; 5)\).
\(d\) n’a pas de coefficient directeur.
Aucune des trois réponses précédentes n’est exacte.
Vous pouvez les tracer si cela vous aide.
Connaissez-vous bien la définition du coefficient directeur d’une droite ? Allez voir la vidéo dans les prérequis.
Question 3
On choisit à nouveau la droite \(d\) d'équation \(x = 5\) et la droite \(d'\) d'équation \(y = 5\).
\(d\) et \(d’\) sont sécantes et non perpendiculaires.
\(d\) et \(d’\) sont perpendiculaires.
\(d’\) n’a pas de coefficient directeur.
Aucune des trois réponses précédentes n’est exacte.
Vous devez savoir tracer des droites d’équations données. Revoyez la vidéo si besoin.
Vous pouvez remarquer que \(y = 5\) s’écrit aussi \(y = 0 \times x +5\).
Question 4
Considérons à présent les droites d'équations :
\(D_1 : y = -2x+7\) et \(D_2 : y= \dfrac{x-5}{2}\)
\(D_1\) et \(D_2\) sont :
parallèles.
on ne sait pas.
sécantes.
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous une condition pour que deux droites soient perpendiculaires ?
Il faut que le produit de leurs coefficient directeur soit égal à -1.
Essayez donc ici... Sait-on jamais.
Réfléchissez ensuite. Des droites perpendiculaires sont-elles sécantes ?
Question 5
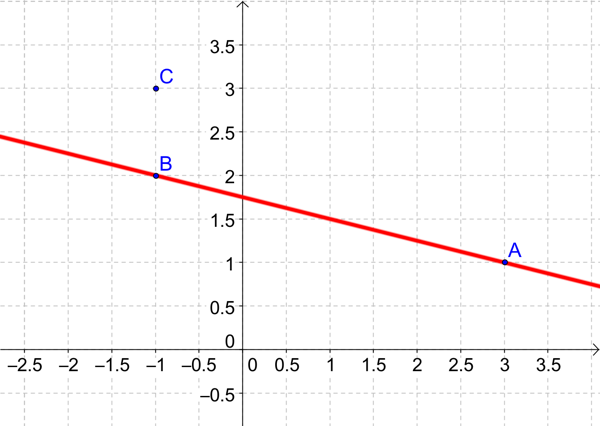
On considère les points \(A(3 ; 1)\) et \(B(-1 ; 2)\) dans un repère orthonormé. Le coefficient directeur de la droite \((AB)\) est :
\(-\dfrac{1}{4}\)
\(\dfrac{1}{4}\)
4
Aucune des trois réponses précédentes n’est exacte.
Vous devez connaître par cœur la formule du cours. C’est la plus importante du chapitre.
Si on note \((AB) : y = ax +b\) alors \(a =\)… ?
\(a=\dfrac{y_B-y_A}{x_B-x_A}\)
\(y_B\) signifie ici l'ordonnée de \(B\) et \(x_A\) l’abscisse de \(A\) bien sûr.
Question 6
Cherchons à présent l'équation réduite de la droite \((AB)\). On sait qu'elle se présente sous la forme \(y = -\dfrac{1}{4}x +b\). Quelle est la valeur de \(b\) ?
\(\dfrac{7}{8}\)
\(\dfrac{4}{7}\)
\(\dfrac{7}{4}\)
Aucune des trois réponses précédentes n’est exacte.
À savoir par cœur : la méthode pour trouver l’équation d’une droite connaissant les coordonnées de deux de ses points. Allez voir la vidéo.
On cherche dans un premier temps (s’il existe) le coefficient directeur. C’est fait, il vaut \(-\dfrac{1}{4}\).
On cherche à présent l’ordonnée à l’origine : le nombre \(b\). Pour cela, on utilise la propriété suivante : Si un point appartient à une droite, ses coordonnées vérifient l’équation de cette droite.
Choisissez \(A\) ou \(B\) et remplacez leurs coordonnées par \(x\) et \(y\) dans l’équation. Vous trouverez alors \(b\).
Question 7
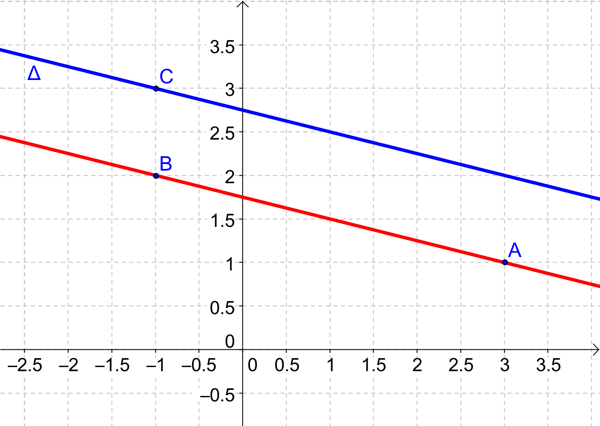
On considère la droite \((AB)\) d'équation \(y = -\dfrac{1}{4}x +\dfrac{7}{4}\) et le point \(C(-1 ; 3)\).
La droite \(\Delta\) parallèle à \((AB)\) passant par \(C\) a pour équation :
\(y = -\dfrac{1}{4}x +\dfrac{1}{4}\)
\(y = 4x +1\)
\(y = -\dfrac{1}{4}x -\dfrac{1}{4}\)
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous une propriété caractéristique des coefficients directeurs de deux droites parallèles ?
Ce sont les mêmes. C’est écrit dans votre cours que vous lisez le soir avant de dormir.
Question 8
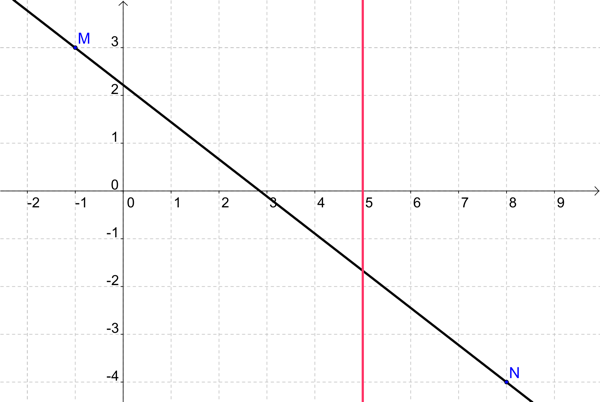
On donne les points \(M(-1 ; 3)\), \(N(8 ; -4)\) et \(X(5 ; a)\) où \(a\) est un réel.
Comment choisir \(a\) pour que les points \(M\), \(N\) et \(X\) soient alignés ?
\(a = \dfrac{5}{3}\)
\(a = -\dfrac{5}{3}\)
\(a = \dfrac{3}{5}\)
Aucune des trois réponses précédentes n’est exacte.
\(M\), \(N\) et \(X\) sont alignés si les droites \((MN)\) et \((NX)\) sont parallèles non ?
Regardez bien : le point \(N\) est commun à ces deux droites. Deux droites parallèles ayant un point commun sont donc confondus. C’est ce qu’il faut pour traduire l’alignement.
Ainsi vous pouvez chercher les coefficients directeurs des deux droites.
Question 9
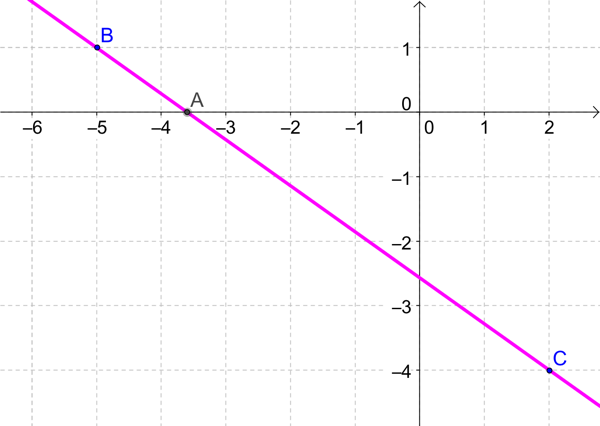
Soit \(B(-5 ; 1)\) et \(C(2 ; -4)\).
Trouver les coordonnées du point \(A\) commun à \((BC)\) et à l'axe des abscisses.
\(A(0 ; \dfrac{38}{7})\)
\(A(-\dfrac{18}{5} ; 0)\)
\(A(0 ; 0)\)
Aucune des trois réponses précédentes n’est exacte.
Le point \(A\) appartient à l’axe des abscisses donc une de ses coordonnées est évidente.
Est-ce A1 ou A2 sur la figure?
Vous pouvez à présent dire que les points \(A\), \(B\) et \(C\) doivent être alignés.
Il suffit alors d’utiliser la méthode vue dans la question précédente pour conclure.
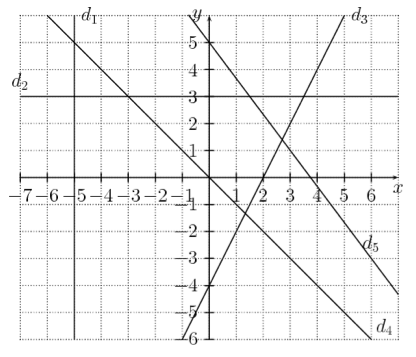
Question 10
Observez bien la représentation graphique ci dessous.
Une seule affirmation est juste. Laquelle ?
Le coefficient directeur de \(d_4\) est 1.
L’équation de droite de \(d_3\) est \(y = 2x-4\) et celle de \(d_1\) est \(y = -5\).
L’équation de droite de \(d_3\) est \(y = -2x-4\) ou celle de \(d_2\) est \(y = 3\).
Aucune des trois réponses précédentes n’est exacte.
Il est probable que vous ayez besoin de chercher les coefficients directeurs de plusieurs droites (si ils existent).
Vous pouvez utiliser le graphique pour lire les ordonnées à l’origine des droites.
Attention aux opérateurs logiques. En mathématiques, ET et OU ont des sens bien spécifiques. Soyez attentif aux phrases.
La droite \(d_1\) est un cas à traiter à part.