Fiche de cours
Points alignés
Deux points étant toujours alignés, on considérera trois points ou plus dans la suite.
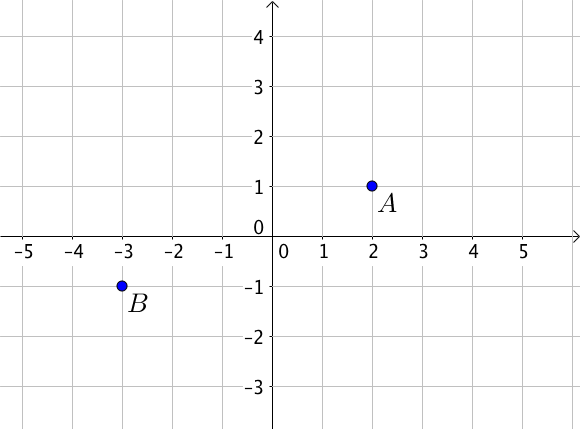
Soient trois points $A(2;1), B(-3; -1)$ et $C(12; 5)$,
On se contente de représenter uniquement les points $A$ et $B$.
Les points $A, B$ et $C$ sont ils alignés ?
Méthode :
Pour répondre à cette question, la méthode consiste à calculer le coefficient directeur de la droite $(AB)$ puis le coefficient de la droite $(AC)$.
Or si ces coefficients directeurs sont égaux, alors les deux droites sont parallèles.
Mais ces deux droites possèdent alors un point commun : $A$, les deux droites sont donc confondues : les points sont donc alignés.
Il faut donc commencer par calculer les deux coefficients directeurs.
Le coefficient directeur de la droite $(AB)$ est :
$a =\dfrac{y_B-Y_A}{x_B-x_A}=\dfrac{-1 -1}{-3 - 2} = \dfrac{2}{5}$.
Le coefficient directeur de la droite $(AC)$ est :<
