La figure ci-dessous représente un cube $ABCDEFGH$.

1) Tracer le plan $(IJK)$ sur la figure. $I$ est le milieu de $[EF]$, $J$ est le milieu de $[AE]$ et $K$ est le milieu de $[BC]$.
2) Citez un plan dont $J$ fait partie, un plan dont $K$ fait partie.
3) Quelle est la nature du triangle $IJK$ ?
4) Démontrer que le triangle $IFK$ est un triangle rectangle en $F$.
5) Que peut-on dire des droites $(CG)$ et $(KF)$ ?
6) Que peut-on dire de la droite $(DB)$ par rapport au plan $(FGH)$ ?
1)
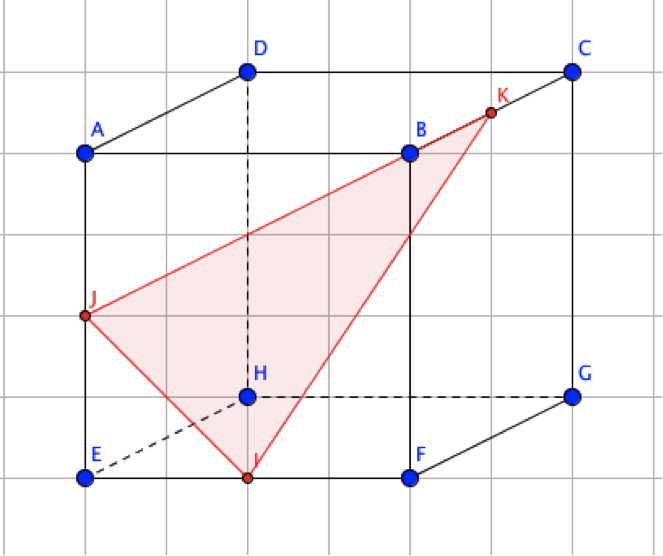
2) $J$ fait partie du plan $(AEH)$ par exemple mais il y en a d’autres : $(ADHE)$, $(ABFE)$, $(ABE)$...
$K$ fait partie du plan $(DCBA)$, $(CBGH)$...
3) $IJK$ est un triangle isocèle car le point $K$ appartient au plan médian de $(IJ)$ donc $IK = JK$.
4) $(IF)$ est perpendiculaire au plan $(FBC)$ et $(FK)$ appartient au plan $(FBC)$ donc on en déduit que $(IF)$ est perpendiculaire à $(FK)$.
$(IFK)$ est un triangle rectangle en $F$.
5) Elles sont sécantes car les points $C, G, K$ et $F$ sont coplanaires et les droites $(CG)$ et $(KF)$ non parallèles.
6) $(DB)$ est parallèle à $(FGH)$.
$(DB)$ appartient à $(ABCD)$ qui est parallèle à $(FGHE)$ et donc à $(FGH)$.
