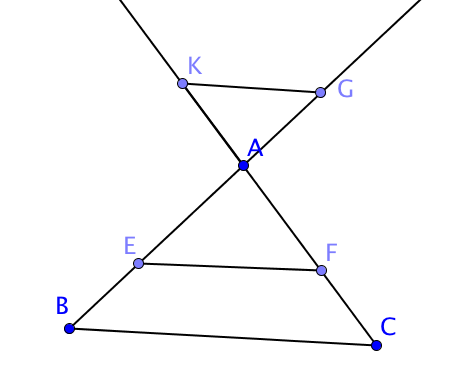
Sur la figure ci-dessus (dimensions non respectées) :
les points $K, A, F, C$ sont alignés
les points $G, A, E, B$ sont alignés
$(EF)$ et $(BC)$ sont parallèles
$AB = 5$ et $AC = 6,5 $
$AE = 3$ et $EF = 4,8 $
$AK = 2,6$ et $AG = 2$
1) Démontrer que $BC = 8$.
2) Les droites $(KG)$ et $(BC)$ sont-elles parallèles ? Justifier.
3) Les droites $(AC)$ et $(AB)$ sont-elles perpendiculaires ? Justifier.
1) Les droites $(EB)$ et $(FC)$ sont sécantes en $A$, les droites $(EF)$ et $(BC)$ sont parallèles.
D'après le théorème de Thalès, on a :
$\dfrac{AE}{AB} = \dfrac{AF}{AC} = \dfrac{EF}{BC}$
Soit : $\dfrac{3}{5} = \dfrac {AF}{6,5} = \dfrac {4,8}{BC}$
Calcul de $BC$ : $\dfrac{3}{5} = \dfrac{4,8}{BC}$
$BC = 4,8 \times \dfrac{5}{3} = 8$
On trouve bien $BC = 8$
2) Les points $K, A, C$ d'une part et $G, A, B$ d'autre part sont alignés dans le même ordre.
On a : $\dfrac{AB}{AG} = \dfrac{5}{2} = 2,5$
Et : $\dfrac{AC}{AK} = \dfrac{6,5}{2,6} = 2,5$
Donc : $\dfrac{AB}{AG} = \dfrac{AC}{AK}$
Donc d'après la réciproque du théorème de Thalès, les droites (KG) et (BC) sont parallèles.
3) Dans le triangle $ABC$, on a :
${BC}^2 = 8^2 = 64$
Et ${AC}^2 + {AB}^2 = {6,5}^2 + 5^2 = 42,25 + 25 = 67,25$
Il apparait que ${BC}^2 \ne {AC}^2 + {AB}^2$ donc d'après le théorème de Pythagore, le triangle $ABC$ n'est pas rectangle en $A$.
Conclusion : les droites $(AC)$ et $(AB)$ ne sont pas perpendiculaires.
