L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Comparer les écritures fractionnaires : $\dfrac{2.5}{10}$ et $\dfrac{1}{4}$
$\dfrac{2.5}{10}<\dfrac{1}{4}$
$\dfrac{2.5}{10}=\dfrac{1}{4}$
$\dfrac{2.5}{10} >\dfrac{1}{4}$
Question 2
Comparer les écritures fractionnaires : $\dfrac{2.5}{5.5}$ et $\dfrac{9}{22}$
$\dfrac{2.5}{5.5}=\dfrac{9}{22}$
$\dfrac{2.5}{5.5}>\dfrac{9}{22}$
$\dfrac{2.5}{5.5}=\dfrac{2.5\times 4}{5.5\times 4}=\dfrac{10}{22}>\dfrac{9}{22}$
$\dfrac{2.5}{5.5}<\dfrac{9}{22}$
Question 3
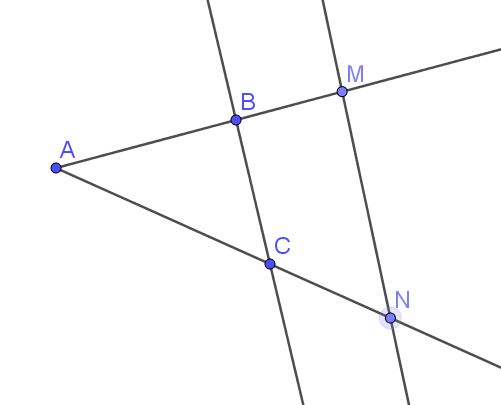
Pour étudier le parallélisme de $(BC)$ et $(MN)$ je dois comparer les rapports :
$\dfrac{AB}{AC}$ et $\dfrac{AM}{AN}$
$\dfrac{AB}{AN}$ et $\dfrac{AC}{AM}$
$\dfrac{AB}{AM}$ et $\dfrac{AC}{AN}$
C'est l'application du cours
Question 4
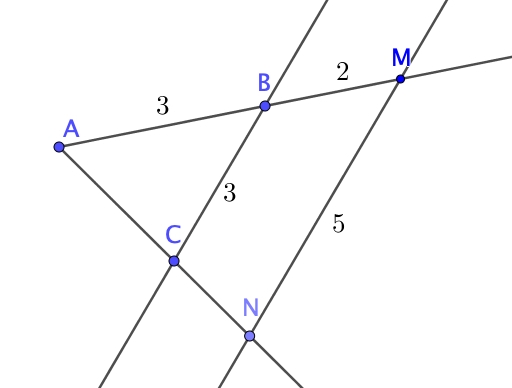
Les droites $(BC)$ et $(MN)$ sont :
sécantes
on ne peut pas répondre
parallèles
En effet : $\dfrac{AB}{AM}=\dfrac{3}{5}=\dfrac{BC}{MN}$
D'après la réciproque de Thalès, les droites sont parallèles
Question 5
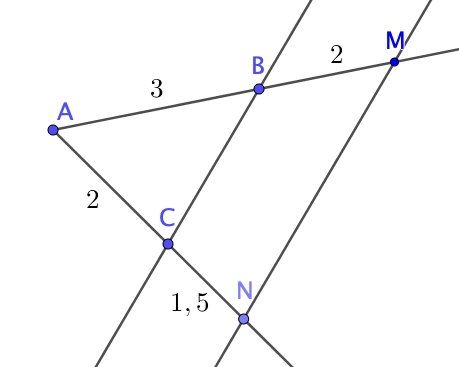
Les droites $(BC)$ et $(MN)$ sont :
sécantes
En effet : $\dfrac{AB}{AM}=\dfrac{3}{5}=\dfrac{21}{35}$
et $\dfrac{AC}{AN}=\dfrac{2}{3.5}=\dfrac{20}{35}$
D'après la contraposée de Thalès, les droites ne sont pas parallèles donc elles sont sécantes.
parallèles
on ne peut pas savoir

$\dfrac{2.5}{10}=\dfrac{2.5\div 2.5}{10\div 2.5}=\dfrac{1}{4}$