L'énoncé
Choisir la ou les bonnes réponses justes parmi celles proposées
Tu as obtenu le score de
Question 1
Parmi les réponses proposées, quel(s) noyau(x) est(sont) instable(s) ?
Un noyau qui possède un surplus d'électrons.
Un noyau qui possède un surplus de protons.
Un noyau auquel il manque des neutrons.
Un noyau qui possède un surplus de protons et de neutrons.
Question 2
Soit une quantité $N_0=120$ noyaux instables présents initialement, combien de noyaux instables reste-t-il au bout de $3 \times t_{1/2}$ ?
60
40
15
0
Question 3
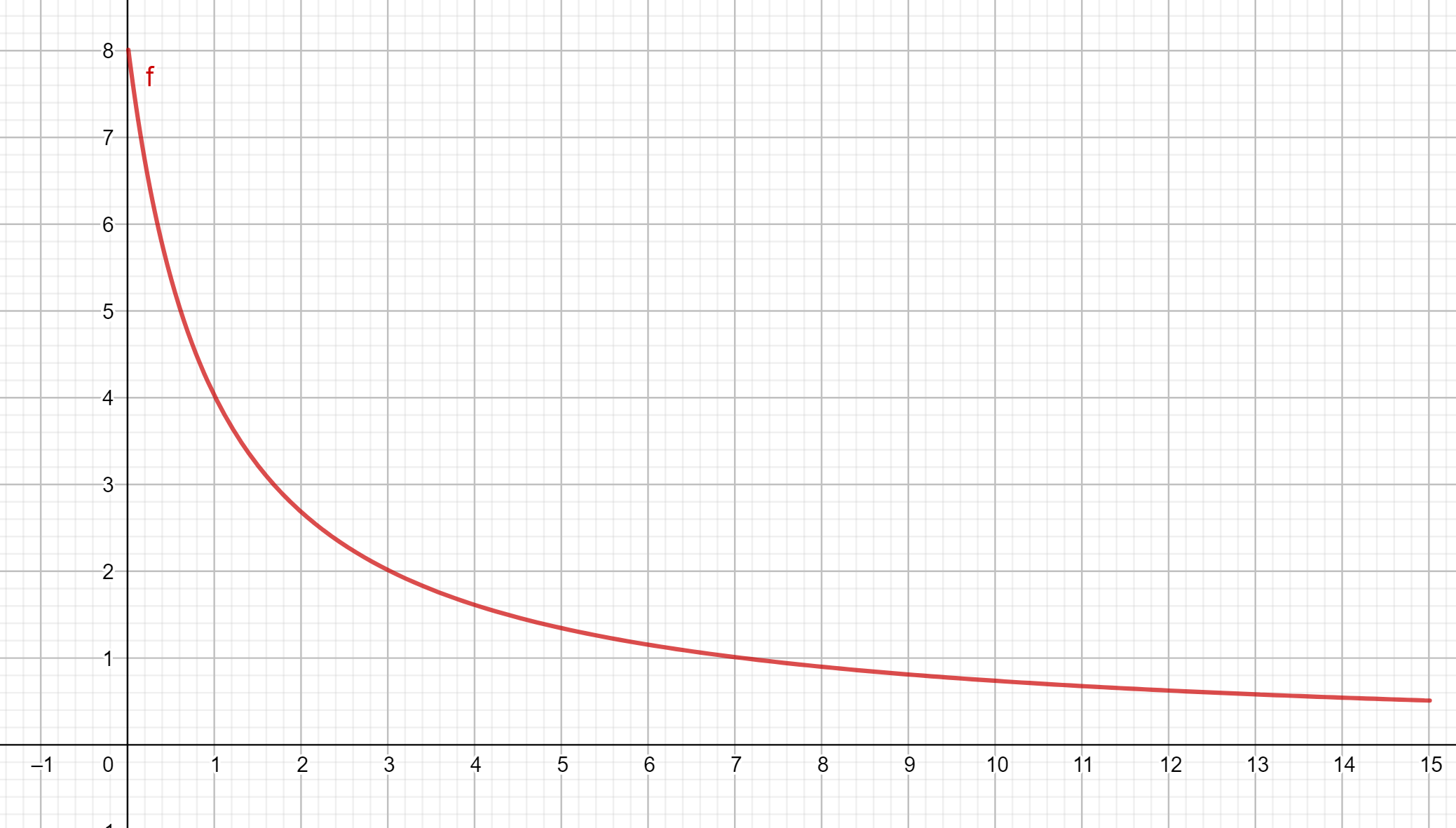
D'après la figure ci-dessous qui représente le nombre de noyaux instables au cours du temps, combien vaut $t_{1/2}$ ?
1
L'abscisse $x$ qui correspond à $f(x)=4$.
f(4)
4
Question 4
D'après la figure ci-dessous qui représente le nombre de noyaux instables au cours du temps, au bout de combien de temps 75 % des noyaux initiaux se sont-il désintégrés ?

$0.3s$
$3s$
Un temps infini.
$2s$
Question 5
D'après la figure ci-dessous qui représente le nombre de noyaux instables au cours du temps, combien de noyaux se sont désintégrés au bout de $6s$ ?

Moins de 5 %.
Plus de 95 %.
60 %.
Entre 96 % et 98 %.
Question 6
Quelle(s) courbe(s) pourrai(en)t correspondre au tracé de la quantité de noyaux instables en fonction du temps ?




Question 7
De quoi dépend le temps de demi-vie $t_{1/2}$ ?
De la quantité de noyaux initiale $N_0$.
De la nature du noyau considéré.
Du nombre d'électrons possédés par les atomes.
De la masse des noyaux.
Question 8
Soit $N_0$ une quantité de noyaux instables initiale, combien de noyaux reste-t-il au bout de $2 \times t_{1/2}$ ?
$\frac{N_0}{2}$.
$\frac{N_0}{2^2}$.
$0.5 \times N_0$.
$\frac{N_0}{4}$.
Question 9
Soit une masse $m=1g$ de noyaux radioactifs $^{14}C$, combien de noyaux initiaux y-a-t-il ? On donne les constantes suivantes :
$M_{C} = 12.01 g.mol^{-1}$ et
$N_a = 6.022 \times 10^{23}.$
$N_0$ = 500.
$N_0 = 5.01 \times 10^{22}$.
$N_0= 50 \times 10^{22}$.
$N_0 = 501 \times 10^{22}$.
Question 10
Soit $N_0=5.01 \times 10^{22}$ noyaux initiaux instables, et soit $t_{1/2}=5.73 \times 10^3 an$ le temps de demi-vie de ces noyaux, combien d'atomes instables reste-il au bout de $4 \times t_{1/2}$ ?
$N = 3.13 \times 10^{21}$.
$N= 2.51 \times 10^{11}$.
$N=0$.
$N=31.3 \times 10^{20}$.