L'énoncé
Un enfant trouve dans un coffre d’un grenier deux jeux datant des années 70, un tac-tac. Ne connaissant pas le principe du tac-tac, il cherche sur Internet et trouve les informations suivantes : le tac-tac est un jouet qui a connu une mode éphémère au début des années 1970. L'objet est constitué de deux boules de plastique dur reliées entre elles par une cordelette d'environ 40 cm de long, au milieu de laquelle un anneau de plastique est fixé par un nœud. En imprimant de légers mouvements à cet anneau, on amène les boules à rebondir l'une contre l'autre en produisant le bruit qui donne son nom au jeu.
D’après francetvinfo.fr
On s’intéresse dans ce sujet au comportement des boules du tac-tac. Le tac-tac est présenté sur la photographie ci-dessous. Dans ce qui suit, on appelle :
- boule 1 la boule située à droite sur la photographie ;
- boule 2 la boule située à gauche sur la photographie.
A. Étude énergétique de la boule 1
On modélise ici le jeu par un pendule simple constitué de la boule 1 de masse m = 80 g, suspendue à un fil inextensible de masse négligeable et de longueur L = 20 cm. Le fil est accroché au point I et les mouvements du pendule s’effectuent dans un plan vertical.
Le joueur écarte la boule 1 d’un angle αm. Le centre de la boule 1 est ainsi situé au point G.
Le joueur lâche la boule 1 sans vitesse initiale.
Le mouvement du pendule est étudié dans le repère (G0, x, z) orienté comme l’indique la figure ci-dessous ; l’axe G0z est vertical. On néglige les frottements.

Données :
- l’énergie potentielle de pesanteur est choisie nulle au point G0 le plus bas de la trajectoire ;
- la valeur de l’intensité de la pesanteur est g = 9,8 N.kg-1.
Question 1
On s’intéresse à la boule 1 lorsqu’elle est à une hauteur $z$ et possède une vitesse $v.$ Rappeler les expressions :
- de son énergie cinétique $Ec$ ;
- de son énergie potentielle de pesanteur $Epp$ ;
- de son énergie mécanique $Em$ en fonction de $m, g, z$ et $v.$
$Ec= \dfrac{1}{2} \times m \times v^2$
$Epp= m \times g \times z$
$Em= Ec + Epp = \dfrac{1}{2} \times m \times v^2 + \times m \times g \times z $
Question 2
On modélise expérimentalement la situation en utilisant un montage comprenant un capteur, un pendule simple de même caractéristique que la partie du tac-tac associée à la boule 1. On peut alors tracer les variations des trois types d'énergie (en mJ) précédentes en fonction de l'abscisse $x$ (en mm) du centre de la boule 1 pour seulement une partie de la trajectoire de la boule 1.
On obtient les courbes suivantes :
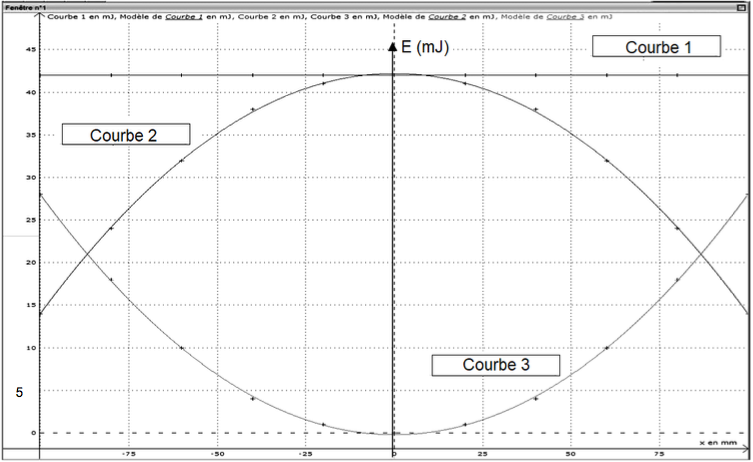
Associer, en justifiant la réponse, chaque courbe à l’énergie $Ec, Epp$ ou $Em$ dont elle représente les variations.
Sur ce graphique, nous avons l’énergie en ordonnée et l’abscisse du centre de la boule en abscisse.
Courbe 1 : c’est une droite horizontale, donc l’énergie est constante quelle que soit l’abscisse de la boule, c’est donc l’énergie mécanique, qui est constante s’il n’y a pas de frottements
Courbe 2 : c’est une courbe croissante puis décroissante. C’est donc l’énergie cinétique car la vitesse augmente jusqu’à une valeur maximale atteinte à l’abscisse $0.$
Courbe 3 : c’est une courbe décroissante puis croissante avec un minimum en $x=0.$ Cela correspond bien à l’énergie potentielle de pesanteur, qui est proportionnelle à $z.$ L’altitude de la boule décroit effectivement jusqu’à l’abscisse $x=0 $ puis croit.
Question 3
B. Étude du choc entre les deux boules
On lâche sans vitesse initiale la boule 1 du point G. Au point G0, un choc se produit entre la boule 1 et la boule 2 qui initialement est au repos. La boule 2 se met en mouvement.
On suppose qu’au point G0 et juste avant le choc la boule 1 possède la vitesse maximale $v_{G0} = 1,0$ m.s-1 et une énergie mécanique de 42 mJ. Au cours du choc entre les deux boules, il se produit une dissipation d'énergie mécanique $E_{dis} = 15$ mJ.
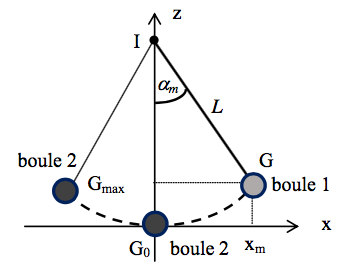
Juste après le choc, la boule 1 est au repos et la boule 2 se met en mouvement vers la gauche pour atteindre, avant de redescendre, un point extrême $G_{max}$ dont on veut déterminer l’altitude $z_{Gmax}.$
Calculer l'énergie mécanique $E_{m2,G0}$ de la boule 2 en $G_0$ juste après le choc.
Au cours du choc, il y a une dissipation d’énergie $E_{dis}.$ On peut donc écrire que l’énergie mécanique totale avant le choc est égale à l’énergie mécanique totale juste après le choc en $G_0$ plus le terme de dissipation $E_{dis}.$
$E_{m1, \ avant} + E_{m2, \ avant} = E_{m1, \ G0} +E_{m2, \ G0} + E_{dis}$
- Après le choc, la boule 1 est au repos à l’altitude $z=0.$ On peut donc calculer son énergie mécanique $ E_{m1, \ G0}=0.$
- Le terme $E_{dis}$ est donné par le sujet $E_{dis}= 15$ mJ.
- Avant le choc, la boule 2 est au repos donc $ E_{m2, \ avant}=0$ J.
- Juste avant le choc, l’énergie mécanique $E_{m1, \ avant}$ est donnée par le sujet $E_{m1, \ avant}=42$ mJ.
On peut donc calculer $E_{m2, \ G0}$ :
$E_{m2, \ G0}= E_{m1, \ avant} + E_{m2, \ avant} - E_{m1, \ avant} - E_{dis}$
$E_{m2, \ G0}=27$ mJ
Question 4
Expliquer pourquoi l’énergie cinétique de la boule 2 au point $G_{max}$ est nulle.
Au point $G_{max}$ la boule va faire demi-tour, cela signifie que sa vitesse est nulle juste au moment de faire demi-tour. En effet, au moment du demi-tour, la composante verticale et horizontale vont changer de signe. Et donc elles vont passer par zéro au moment précis du demi-tour.
L’énergie cinétique étant proportionnelle à la vitesse au carré, elle est nulle aussi.
Question 5
Exprimer l'énergie mécanique $ E_{m2, \ Gmax}$ de la boule 2 au point $G_{max}$ en fonction de $m, g$ et $z_{Gmax}.$
$ E_{m2, \ Gmax} =E_{c2, \ Gmax} +E_{pp2, \ Gmax} $
Puisque $E_{c2, \ Gmax}=0$
$ E_{m2, \ Gmax} =E_{pp2, \ Gmax} = m \times g \times z_{Gmax}$
Question 6
En supposant que l'énergie mécanique de la boule 2 reste constante au cours de son mouvement, calculer la valeur de l’altitude $z_{Gmax}.$ Conclure.
Comme l’énergie mécanique de la boule 2 est constante :
$ E_{m2, \ G0} = E_{m2, \ Gmax}$
Soit $ E_{m2, \ G0} = m \times g \times z_{Gmax}$
Donc $z_{Gmax} = \dfrac{E_{m2, \ G0}}{m \times g}=3,4.10^{-2}$ m
Le transfert d’énergie de la boule 1 à la boule 2 a donc permis à la boule 2 de monter à son tour. Elle va ensuite redescendre et entrer de nouveau en collision avec la boule 1.
On pourrait aussi rajouter comme commentaire une comparaison avec la hauteur initiale de la boule 1. Mais nous n’en avons pas calculé la valeur. C’est néanmoins faisable car l’énergie mécanique de la boule 1 valait 42 mJ. Or à l’instant initial, elle n’avait pas de vitesse initiale donc son altitude valait, en reprenant la formule de la question précédente $z_{1 \ initiale} = \dfrac{E_{m1, \ initiale}}{m \times g}= 5,4.10^{-2}$ m.
On peut donc dire que la boule 2 monte moins haut et c’est tout à fait normal car il y a eu une perte énergétique lors du choc donc le transfert d’énergie n’a pas été optimal.
