Sur un cercle trigonométrique de centre $O$, les points $A$, $B$, $C$ et $D$ sont les images respectives des réels $0$ ; $\dfrac{\pi}{3}$ ; $\dfrac{3 \pi}{4}$ ; $- \dfrac{\pi}{6}$
1) Placer les points $A$, $B$, $C$ et $D$ sur le cercle.
2) Donner une mesure en radian de chaque angle :
A) $(\overrightarrow{OA} ; \overrightarrow{OB})$
B) $(\overrightarrow{OC} ; \overrightarrow{OD})$
C) $(\overrightarrow{OD} ; \overrightarrow{OB})$
3) Donner les sinus et cosinus de $(\overrightarrow{OA} ; \overrightarrow{OB})$ et $(\overrightarrow{OD} ; \overrightarrow{OB})$
1)
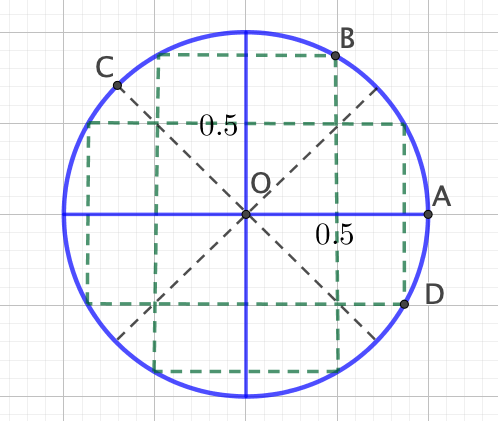
2) A) $(\overrightarrow{OA} ; \overrightarrow{OB}) = \dfrac{\pi}{3} - 0 = \dfrac{\pi}{3}$ $[2\pi]$
B) $(\overrightarrow{OC} ; \overrightarrow{OD}) = - \dfrac{\pi}{6} - \dfrac{3\pi}{4} = - \dfrac{2\pi}{12} - \dfrac{9\pi}{12} = \dfrac{-11 \pi}{12}$ $[2\pi]$
C) $(\overrightarrow{OD} ; \overrightarrow{OB}) =\dfrac{\pi}{3} - \left( {-\dfrac{\pi}{6}} \right) = \dfrac{2 \pi}{6} - \left( {- \dfrac{\pi}{6}} \right) = \dfrac{3 \pi}{6} = \dfrac{\pi}{2}$ $[2\pi]$
3) $(\vec{OA} ; \vec{OB}) = \dfrac{\pi}{3}$ $[2\pi]$
Alors on a :
$\left\{ \begin{array}{ll} {\cos \left( {\dfrac{\pi}{3}} \right) = \dfrac{1}{2} \\ \sin \left( {\dfrac{\pi}{3}} \right) = \dfrac{\sqrt{3}}{2} } \end{array} \right.$
$(\vec{OD} ; \vec{OB}) = \dfrac{\pi}{2}$ $[2\pi]$
Alors on a :
$\left\{ \begin{array}{ll}{\cos \left( {\dfrac{\pi}{2}} \right) = 0 \\ \sin \left( {\dfrac{\pi}{2}} \right) = 1 } \end{array} \right.$
