L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
On note $O$ l'origine d'un repère. Qu'est ce que le cercle trigonométrique ?
Un cercle de centre $O$ et de rayon quelconque.
Un cercle de centre quelconque et de rayon $1$.
N'importe quel cercle.
Le cercle de centre $O$ et de rayon $1$.
Question 2
Quel est le sens d'orientation direct du cercle trigonométrique ?
Sens horaire
Sens anti-horaire
Ça dépend
Il s'agit toujours du sens anti-horaire
Question 3

On reprend le schéma avec un cercle et une droite $D$ tangente au cercle en un point de coordonnées $(1;0)$.
On enroule cette droite autour du cercle.
À combien de points du cercle correspond un point $N$ de la droite ?
Un point
Plusieurs points
Aucun
Lorsqu'on enroule la droite sur le cercle le point $N$ correspond à un unique point $M$ du cercle.
Question 4
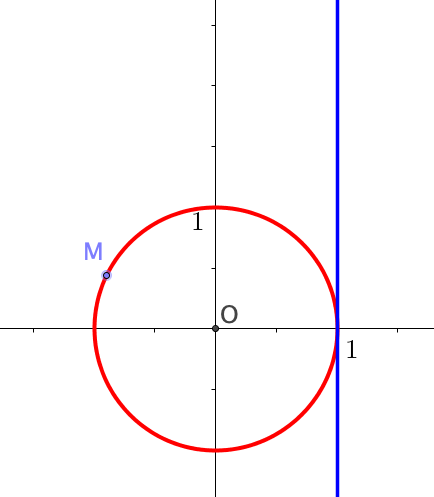
On reprend le schéma avec un cercle et une droite $D$ tangente au cercle en un point de coordonnées $(1;0)$.
À combien de points de la droite correspond un point $M$ du cercle ?
Un point
Plusieurs points
Aucun
On peut enrouler la droite autour du cercle et faire plusieurs tours et dans les deux sens, un point $M$ du cercle correspond donc à plusieurs points sur la droite.
Question 5
Quelle est la distance entre deux points consécutifs de la droite $D$ enroulée autour du cercle correspondant au même point $M$ sur le cercle ?

$\pi$
$2\pi$
$3\pi$
Entre deux points consécutifs on a réalisé un tour de cercle donc la distance est $2\pi$.
Question 6
À combien de radians correspondent 60° ?
$\dfrac{\pi}{3}$
$\dfrac{\pi}{4}$
$\dfrac{\pi}{6}$
Il existe une relation de proportionnalité entre les radians et les degrés.
$2\pi$ correspond à 360°, on en déduit donc le résultat avec un tableau de proportionnalité.
Question 7
À combien de radians correspondent 30° ?
$\dfrac{\pi}{3}$
$\dfrac{\pi}{4}$
$\dfrac{\pi}{6}$
Il existe une relation de proportionnalité entre les radians et les degrés.
$2\pi$ correspond à 360°, on en déduit donc le résultat avec un tableau de proportionnalité.
Question 8
À combien de degré correspondent $\dfrac{\pi}{4}$ ?
40°
45°
50°
Il existe une relation de proportionnalité entre les radians et les degrés.
$2\pi$ correspond à 360°, on en déduit donc le résultat avec un tableau de proportionnalité.
Question 9
À combien de degré correspondent $\dfrac{\pi}{9}$ ?
20°
25°
15°
Il existe une relation de proportionnalité entre les radians et les degrés.
$2\pi$ correspond à 360°, on en déduit donc le résultat avec un tableau de proportionnalité.
Question 10
À combien de radians correspondent 15° ?
$\dfrac{\pi}{10}$
$\dfrac{\pi}{11}$
$\dfrac{\pi}{12}$
Il existe une relation de proportionnalité entre les radians et les degrés.
$2\pi$ correspond à 360°, on en déduit donc le résultat avec un tableau de proportionnalité.
