Fiche de cours
Cercle trigonométrique - longueur d'arc - radian
I - Cercle trigonométrique et longueur d'arc
Définition :
On appelle cercle trigonométrique noté $\mathcal{C}(O; 1)$ le cercle de centre $O$ et de rayon 1, orienté dans le sens direct (c'est à dire le sens anti-horaire ou bien le sens inverse des aiguilles d'une montre).
Son périmètre vaut $P = D \times \pi = 2 \pi$.
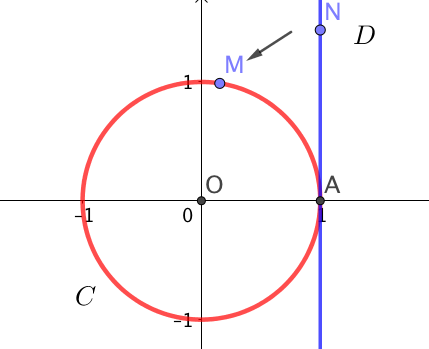
On trace la droite des réels tangente au cercle trigonométrique au point $(1;0)$.
Par enroulement de la droite réelle $\mathcal{D}$ sur le cercle trigonométrique, on obtient les résultats suivants :
- A tout réel $x$ de la droite et en notant $N$ le point correspondant, on associe un point $M$ unique sur ce cercle.
La longueur de l'arc $\overset{\frown}{AM}$ est exactement égale à la longueur $AN$.
- A tout point $M$ du cercle est associé une infinité de réels.
En effet, si $x$ est un réel, on obtient un autre réel sur la droite en écrivant $x + 2k \pi$, avec $k$ entier.
