Cours Échantillonnage
lesbonsprofs.com
Image
Cours Échantillonnage
1
Video Intervalle de fluctuation
2
Exercice QCM - Intervalle de fluctuation
3
Exercice Loi binomiale et intervalle de fluctuation
4
Video Echantillonnage
5
Exercice Exercice - Intervalle de confiance
QCM
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

L'énoncé

Cet exercice est un QCM ; il n’y a qu’une seule bonne réponse possible parmi toutes celles proposées.

Tu as obtenu le score de

Question 1

On lance 1 000 fois un dé équilibré. La fréquence de nombres "pairs" obtenus appartient à l'intervalle de fluctuation :

\(I_f = \left[ 0,5 - \dfrac{1}{\sqrt{1000}} ; 0,5 + \dfrac{1}{\sqrt{1000}} \right]\)

Jamais.

Au seuil de 95%.

Toujours.

Au seuil de 5%.

Evident ; c'est une définition de cours !

Question 2

La probabilité qu'une personne ait les yeux bleus en France est de 0,32. On s'intéresse à un échantillon de 375 personnes. Quel est l'intervalle de fluctuation au seuil de 95% ?

\(I_f = [0,27 ; 0,37]\)

On utilise la propriété du cours \(\large I_f = \left[ p - \frac{1}{\sqrt{n}} ; p + \frac{1}{\sqrt{n}} \right]\) avec ici \(p = 0,32\) (c’est la probabilité) et \(n = 375\) (c’est le nombre d’individus dans l’échantillon)

\(I_f = [0,31 ; 0,32]\)

\(I_f = [3,15 ; 3,25]\)

On ne peut pas savoir.

\( I_f = \left[ p - \dfrac{1}{\sqrt{n}} ; p + \dfrac{1}{\sqrt{n}} \right]\)


Ici, que vaut \(p\) ?


Que vaut \(n\) ?

Question 3

On lance 100 fois une pièce de monnaie non truquée. A quel intervalle de fluctuation au seuil de 95% appartient la fréquence de "face" obtenue ?

\(I_f = [98,6 ; 101,4]\)

\(I_f = [0,49 ; 0,51]\)

\(I_f = [0,4 ; 0,6]\)

C’est la formule du cours \( I_f = \left[ p - \dfrac{1}{\sqrt{n}} ; p + \dfrac{1}{\sqrt{n}} \right]\) avec ici \(p = 0,5\) (probabilité d’obtenir Face) et \(n = 100\).

On ne peut pas savoir.

L'intervalle cherché est : \( I_f = \left[ p - \dfrac{1}{\sqrt{n}} ; p + \dfrac{1}{\sqrt{n}} \right]\)


Que vaut \(p\) ? C'est-à-dire la probabilité d'obtenir "face" en un lancer ?


Que vaut \(n\) ? C'est-à-dire la taille de l'échantillon ou encore le nombre de lancers ?

Question 4

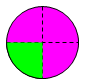
On lance 10 000 fois cette roue où le secteur vert est le secteur gagnant.



Quel est l'intervalle de fluctuation au seuil de 95% de la fréquence des gains ?
\(I_f = [0,2499 ; 0,2501]\)
\(I_f = [0,24 ; 0,26]\)
Ici on a \(p = \frac{1}{4} = 0,25\) (le secteur gagnant correspond en effet à un quart de cercle) et \(n = 10 000\).
\(I_f = [10,4 ; 10,6]\)
On ne peut pas savoir.
\(\large I_f = \left[ p - \frac{1}{\sqrt{n}} ; p + \frac{1}{\sqrt{n}} \right]\) avec ici \(p = 0,5\)
Ici, que vaut \(p\) ?
Que vaut \(n\) ?

Question 5

Un sac contient 30% de jetons verts. On tire n fois et avec remise un jeton dans ce sac. L'intervalle de fluctuation de la fréquence des jetons verts au seuil de 95% est de \([0,2 ; 0,4]\). Quel est le nombre n de tirages effectués ?
\(n = 40\)
\(n = 50\)
\(n = 100\)
En effet, on ici \(p = \frac{3}{100} = 0,3\) (30% de chance d’obtenir un jeton vert). De plus, on a aussi que : \(p - \frac{1}{\sqrt{n}} =0,2\) (c’est la première borne de l’intervalle) soit \(0,3 - \frac{1}{\sqrt{n}} =0,2\)
Donc : \(0,3 - 0,2= \frac{1}{\sqrt{n}}\) soit \(\frac{1}{\sqrt{n}} = 0,1\) donc \(\sqrt{n}=\frac{1}{0,1} = 10\) et \(n = 100\).
On ne peut pas savoir.
\(\large I_f = \left[ p - \frac{1}{\sqrt{n}} ; p + \frac{1}{\sqrt{n}} \right]\)
Que vaut \(p\) ? C'est-à-dire la probabilité d'obtenir "un jeton vert" en un lancer ?
D'après l'énoncé que vaut \(p-\frac{1}{\sqrt{n}}\) ?
On peut alors remplacer n par les différentes valeurs proposées et vérifier pour laquelle on obtient l'intervalle de fluctuation donné. On peut aussi résoudre une équation qui donnera la valeur de \(n\) ; c'est la méthode qu'il faudrait utiliser dans un exercice hors QCM.

Question 6

La proportion d'hommes inscrits dans une association caritative est de 0,45. Lors d'une réunion de 25 personnes de cette association :
Il y a entre 6 et 17 hommes.
Voilà pourquoi :
Ici \(p = 0,45\) et \(n = 25\).
L’intervalle de fluctuation est \(\large I_f = \left[ p - \frac{1}{\sqrt{n}} ; p + \frac{1}{\sqrt{n}} \right]\) : cela correspond concrètement à l’intervalle dans lequel fluctue la fréquence du nombre d'hommes.

Alors : \(p - \frac{1}{\sqrt{n}} = 0,45 - \frac{1}{\sqrt{25}} = 0,45-0,2= 0,25\)
Et : \(p + \frac{1}{\sqrt{n}} = 0,45 + \frac{1}{\sqrt{25}} = 0,45+0,2= 0,65\)

La fréquence du nombre d’hommes fluctue donc entre 0,25 et 0,65 (en pourcentage cela donne 25% et 65%).
Comme il y a 25 personnes au total, le nombre d’hommes fluctue entre \(\frac{25}{100} \times 25 = 6,25\) et \(\frac{65}{100} \times 25 = 16,25\)
Soit entre 6 et 17 hommes.
Il y a au plus 6 hommes.
Il peut y avoir au moins 20 hommes.
Aucune des propositions n'est correcte.
Que vaut \(p\) ?
Que vaut \(n\) ?
Dans quel intervalle fluctue la fréquence du nombre d'hommes ?
Il y a 25 personnes ; dans quel intervalle fluctue le nombre d'hommes ?

Question 7

Dans un tableur la formule "= 1+ENT(6*ALEA())" donne :
Un nombre entier aléatoire entre 0 et 5.
Un nombre entier aléatoire qui est 0 ou 1.
Un nombre entier aléatoire entre 1 et 6.
En effet, ALEA() donne un nombre réel aléatoire strictement compris entre 0 et 1, et donc 6*ALEA() donne un nombre réel aléatoire strictement compris entre 0 et 6.

ENT(6*ALEA()) prend la partie entière de "6*ALEA()" et donne donc un nombre entier aléatoire compris entre 0 et 5 (si tu ne comprends pas la notions de « partie entière » voici quelques exemples, c’est tout simple : la partie entière de 1,4 et 1, celle de 4,8 est 4, celle de 5,6 est 5, ainsi de suite… : on ne garde que le nombre entier, et pas les chiffres après la virgule).

Au final, 1+ENT(6*ALEA()) donne donc un nombre entier compris entre 1 et 6.
Un nombre entier aléatoire qui est 1 ou 2.
Tester sur un tableur !
ALEA() donne un nombre réel aléatoire strictement compris entre 0 et 1.
6*ALEA() donne un nombre réel aléatoire strictement compris entre 0 et 6.
ENT(6*ALEA()) prend la partie entière de "6*ALEA()" et donne donc un nombre entier aléatoire compris entre 0 et 5.
1+ENT(6*ALEA()) donne donc un nombre entier…

Question 8

48% des 1 000 personnes interrogées lors dun sondage ont déclaré vouloir voter pour le candidat A.
Une estimation du pourcentage des voix recueillies par le candidat, obtenue par un intervalle de confiance au seuil de 95% est :
\([44,8 ; 51,2]\)
Ici \(f = 0,48\) (c’est la fréquence observée) et \(n = 1 000\), puis on applique la formule sur l’intervalle de confiance : \(\large I_c = \left[ f - \frac{1}{\sqrt{n}} ; f + \frac{1}{\sqrt{n}} \right]\).
On obtient l’intervalle de confiance \([0,448 ; 0,512]\) : une estimation du pourcentage de voix est donc dans l’intervalle de confiance : \([44,8 ; 51,2]\).
\([47,9 ; 48,1]\)
\([53,5 ; 53,8]\)
On ne peut pas savoir.
\(\large I_c = \left[ f - \frac{1}{\sqrt{n}} ; f + \frac{1}{\sqrt{n}} \right]\)
Que vaut \(n\) ?
Que vaut \(f\) ?

Question 9

Le taux d'audience dune chaîne de télévision, un soir à vingt heures, a été mesuré à partir de 1000 appareils ; on a trouvé 31%. Quelle est une estimation de l'audience de cette chaîne ce soir-là pour le pays entier ?

Entre 27,8% et 34%.

Ici \(n = 1 000\) et la fréquence observée est \(f = 0,31\).
L’intervalle de confiance est donc : \(\large I_c = \left[ f - \frac{1}{\sqrt{n}} ; f + \frac{1}{\sqrt{n}} \right]\) soit \(I_C = [0,278 ; 0,34]\). En repassant aux pourcentages on a : 27,8% et 34%.

Entre 30,9% et 31,1%.

Entre 9,69% et 10,31%.

On ne peut pas savoir.

Que vaut \(n\) ?


31% représente une probabilité théorique ou bien une fréquence observée ?


On cherche l'intervalle de confiance ou bien de fluctuation ?

Question 10

Lors dun sondage effectué aux États-Unis en 1995, sur 737 fumeurs quotidiens, seuls 295 estimèrent courir un risque de cancer supérieur à celui des non fumeurs de leur âge. Une estimation de la proportion p de fumeurs aux États-Unis pensant prendre un risque est :
\([0,398 ; 0,401]\)
\([0,36 ; 0,44]\)
La fréquence \(f\) des fumeurs interrogés pensant prendre un risque est égale à \(f = \frac{295}{737} = 0,400\) environ.
L’intervalle de confiance est alors \(\large I_c = \left[ f - \frac{1}{\sqrt{n}} ; f + \frac{1}{\sqrt{n}} \right]\) avec \(f- \frac{1}{\sqrt{n}} = 0,400 - \frac{1}{\sqrt{737}} \approx 0,363\) et aussi \(f+ \frac{1}{\sqrt{n}} = 0,400 + \frac{1}{\sqrt{737}} \approx 0,437\), donc \(I_C = [0,36 ; 0,44]\).
\([73,5 ; 73,8]\)
On ne peut pas savoir.
Quelle est la fréquence \(f\) des fumeurs interrogés pensant prendre un risque ?
Que vaut \(n\) ?
On cherche l'intervalle de confiance ou bien de fluctuation ?