L'énoncé
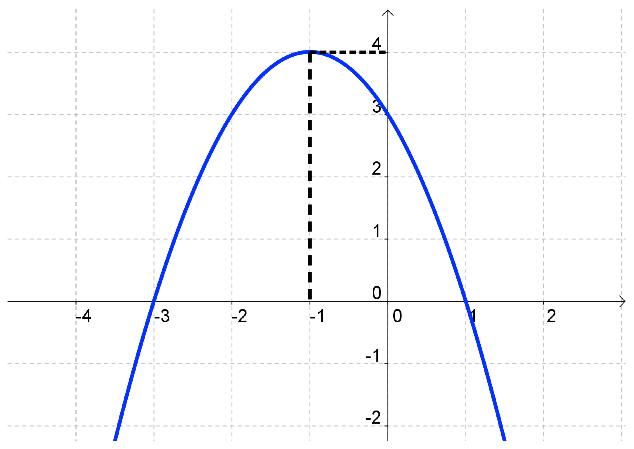
La parabole ci-dessous est la représentation graphique d’une fonction polynôme de degré 2 de forme canonique : \(f(x) = a(x – \alpha)^2 + \beta \)
Question 1
Déterminer \(\alpha\) et \(\beta\) puis donner l'expression de \(f(x)\) en fonction de \( a\).
\(\alpha\) et \(\beta\) sont les coordonnées du sommet de la parabole. On a donc : \(\alpha = - 1\) et \(\beta = 4\).
On en déduit que \(f(x) = a(x + 1)^2 + 4\)
Que représentent \(\alpha\) et \(\beta\) pour une parabole ?
On peut donc les lire !
Question 2
Calculer \(a\).
Graphiquement on a \( f(0) = 3\)
De plus, \(f(x) = a(x + 1)^2 + 4\) donc
\(f(0) = a(0 + 1)^2 + 4 = a + 4\).
Par conséquent : \(a + 4 = 3\) soit \(a = - 1\).
Que vaut, graphiquement \(f(0)\) ?
Et par le calcul ?
On peut donc conclure !
Question 3
En déduire l'expression développée et réduite de \(f\).
Pour tous réels \(x\),
\( \begin{align*} f(x) = -(x + 1)^2 + 4 &\Leftrightarrow f(x) = -(x^2 + 2x + 1) + 4 \\ &\Leftrightarrow f(x) = -x^2 - 2x + 3 \end{align*}\)
Quelle est la forme canonique de \(f\) ?
Il n'y a plus qu’à la développer !
Question 4
Déterminer la forme factorisée de \(f\).
Pour tous réels \(x\), \(f(x) = -x^2 - 2x + 3\).
Soit \(\Delta\) son discriminant.
On a \(\Delta = 16\) donc deux racines \(-3\) et \(1\).
Ainsi, pour tous réels \(x\),
\(f(x) = - (x +3)(x - 1)\).
Commence par calculer le discriminant et applique ton cours.
\(f(x) = a(x – x_1)(x - x_2) \) avec \(x_1\) et \(x_2\) les deux racines de \(f\).
Question 5
Déterminer le signe de \(f(x)\).
\(f\) admet deux racines. \(f(x)\) est donc du signe de \(a = -1\) soit négatif à l'extérieur des racines et positif entre les racines. On écrit aussi :
- Pour \(x \in ] -\infty ; -3[ \cup ]1 ; +\infty [, f(x) < 0\)
- Pour \(x \in ]-3 ;1[, f(x) > 0\)
- Pour \(x = - 3\) ou \(x = 1, f(x) = 0\)
Le signe dépend du nombre de racines et du signe \(a\).
Question 6
On considère la fonction \(g\) définie sur \(\mathbb{R}\) par \(g(x) = 3x^2 - 10x - 9\).
Déterminer la position relative des courbes \(C_f\) et \(C_g\) représentant respectivement les fonctions \(f\) et \(g\)
Pour tous réels \(x\) on a :
\( \begin{align*} f(x) - g(x) = -x^2 - 2x + 3 - (3x^2 - 10x - 9) &\Leftrightarrow f(x) - g(x) = -x^2 - 2x + 3 - 3x^2 + 10x + 9 \\ &\Leftrightarrow f(x) - g(x) = -4x^2 + 8x + 12 \end{align*} \)
Soit \(\Delta\) le discriminant de ce trinôme.
On a \(\Delta = 256\) donc le trinôme admet deux racines \(3\) et \(-1\).
Ainsi, \(f(x) - g(x)\) est du signe de \(a = -4\) soit négatif à l'extérieur des racines et positif entre les racines.
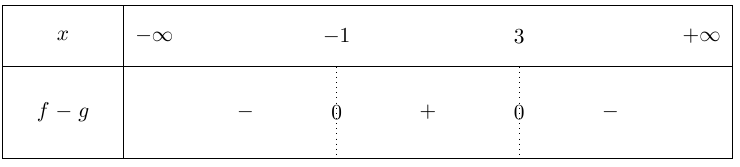
On en déduit que :
- Sur \( ] -\infty; -1[\) et sur \( ]3 ; +\infty [ \ C_f\) est au-dessous de \(C_g\).
- Sur \( ]-1 ; 3[ \ C_f\) est au-dessus de \(C_g\).
- \(C_f\) et \(C_g\) sont sécantes en \(x = - 1\) et \(x = 3\).
Il faut déterminer le signe de \(f(x) – g(x)\).
Commencee par calculer \(f(x) – g(x)\). Son signe est (sûrement) celui d’un trinôme du second degré !