L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
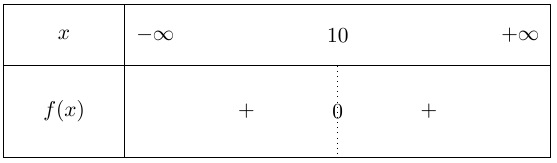
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = ax^2 + bx + c\) avec \(a \neq 0\) dont le tableau de signes est donné ci-dessus et \(\Delta\) son discriminant. Alors :
\(a < 0\) et \(\Delta = 0\)
\(a < 0\) et \(\Delta < 0\)
\(a > 0\) et \(\Delta = 0\)
\(a > 0\) et \(\Delta > 0\)
Combien de racines possède \(f\) ?
Donc de quel signe est \(\Delta\) ?
La parabole peut-elle être tournée vers le haut ? Vers le bas ?
De quel signe est \(a\) ?
\(f\) a une racine donc \(\Delta = 0\). De plus \(f\) étant positive sur \(\mathbb{R}\), sa parabole est tournée vers le haut et donc \(a > 0\).
Question 2
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = -7x^2 +14x -7\) et \(C_f\) sa parabole associée dans un repère du plan. Alors :
\(C_f\) est au-dessus de l'axe des abscisses \((Ox)\).
\(C_f\) est au-dessous de l'axe des abscisses \((Ox)\).
\(C_f\) et \((Ox)\) sont sécants en un point unique.
\(C_f\) et \((Ox)\) sont sécants en deux points distincts.
Que représentent pour \(f\) les abscisses des points d'intersection de \(C_f\) et de l'axe \((Ox)\) ?
Plus généralement quel est le signe de \(f(x)\) ?
On a \(\Delta = 0\) donc \(C_f\) et \((Ox)\) sont sécants en un point unique.
De plus \(f(x)\) est du signe de \(a = -7\) à savoir négatif donc \(C_f\) est au-dessous de l'axe des abscisses \((Ox)\).
Question 3
Dans un repère du plan on considère la parabole \(P\) et la droite \(D\) d'équations respectives \(y = -4x^2 - 10x + 9\) et \(y = -2x +17\)
\(P\) est au-dessus de \(D\) sur \(\mathbb{R}\).
\(P\) est au-dessous de \(D\) sur \(\mathbb{R}\).
\(P\) et \(D\) sont sécantes en un unique point sur \(\mathbb{R}\).
\(P\) et \(D\) sont sécantes en deux points distincts sur \(\mathbb{R}\).
Pour déterminer la position de deux courbes il faut étudier le signe de la différence des deux équations associées.
On résout sur \(\mathbb{R} : -4x^2 - 10x + 9 = -2x + 17 \Leftrightarrow -4x^2 - 8x – 8 = 0\)
On a \(\Delta = -64\) donc le trinôme \(-4x^2 - 8x – 8\) n'a aucune racine et l'équation \( -4x^2 - 8x – 8= 0\) n'a aucune solution. Ainsi \(P\) et \(D\) ne peuvent être sécantes.
\(-4x^2 - 8x – 8\) est toujours négatif car du signe de \(a = -4\) et donc \(P\) est au-dessous de \(D\) sur \(\mathbb{R}\).
Question 4
L'inéquation \(-3x^2 + 9x + 5 \geq -x^2 - 2x + 17 \) a pour ensemble solution :
\(S = \left[\dfrac{3}{2} ; 4\right]\)
\(S =\left] \dfrac{3}{2} ; 4\right[\)
\(S = \left] -\infty; \dfrac{3}{2}\right[\cup ]4 ; +\infty[\)
\(S =\mathbb{R}\)
Il faut se ramener à un trinôme du second degré.
Étudie alors le signe de ce trinôme.
Si besoin dresse un tableau de signes.
On résout \(-2x^2 + 11x – 12 \geq 0\)
On a \(\Delta = 25\) donc deux racines \(\dfrac{3}{2}\) et \(4\). Le trinôme est donc du signe opposé de \(a = -2\) soit positif entre les racines.
Attention : une fois encore \(>\) et \(\geq\) ne donnent pas le même ensemble solution.
Question 5
Dans un repère du plan on considère les paraboles \(C_f\) et \(C_g\) d'équations respectives : \(y = 10x^2 + 8 \) et \(y = - 7x^2 + 20x - 7\)
Sur \(\left]-1; \dfrac{4}{15}\right[\) uniquement \(C_f \) est au-dessus de \(C_g\).
Sur \(]-\infty ; -1[ \) uniquement \( C_f \) est au-dessus de \(C_g\).
Sur \(\left] \dfrac{4}{15};+\infty\right[\) uniquement \( C_f \) est au-dessus de \(C_g\).
Sur \(\mathbb{R}, \ C_f \) est au-dessus de \(C_g\).
Il faut déterminer la position relative de \(C_f\) et \(C_g\).
Quelle inéquation faut-il résoudre ?
Quel est son signe ?
On étudie le signe de \(10x² + 8 - (- 7x^2 + 20x - 7)\) soit de \(17x^2 - 20x + 15\).
On a \(\Delta = - 620\) donc :
- Le trinôme n'a aucune racine (\(C_f\) et \(C_g\) ne sont pas sécantes).
- Le trinôme est toujours positif (du signe de \(a\)).
