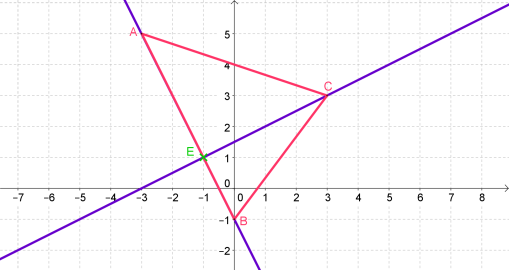
L'énoncé
Dans tout cet exercice on se place dans un repère du plan. On considère les points \(A(-3;5)\) \(B(0;-1)\) et \(C(3;3)\).
Question 1
Déterminer une équation de la droite \((AB)\).
\(\overrightarrow{AB}\begin{pmatrix} -3 \\ -6 \end{pmatrix}\) est un vecteur directeur de \((AB)\) donc \((AB)\) a pour équation :
\(ax + by +c = 0\) avec \( b =- 3\) et \(a = -6\).
Ainsi : \((AB)\) : \(-6x - 3y + c = 0\)
De plus \(A(-3;5) \in (AB) \Leftrightarrow -6x_A - 3y_A + c = 0 \Leftrightarrow c = -3\).
Donc, une équation de la droite \((AB)\) est \(-6x - 3y - 3 = 0\) ou encore \(2x + y + 1 = 0\)
Peux-tu trouver un vecteur normal à \((AB)\) ? Un vecteur directeur ?
Quel(s) point(s) appartient à cette droite ?
Question 2
Déterminer un vecteur normal \(\overrightarrow{n_1} \) à la droite \((AB)\).
Une équation de la droite \((AB)\) est \(2x + y + 1 = 0\) donc un vecteur normal à \((AB)\) est \(\overrightarrow{n_1}\begin{pmatrix} 2 \\ 1\end{pmatrix}\)
Relire le cours ! La réponse y est écrite.
Question 3
Soit \((d)\) la droite perpendiculaire à \((AB)\) et passant par \(C\).
Donner un vecteur \(\overrightarrow{u}\) directeur de \((d)\) et un vecteur normal \(\overrightarrow{n_2}\) de \((d)\).
\((d)\) est perpendiculaire à la droite \((AB)\) donc un vecteur directeur de \((d)\) est un vecteur normal à \((AB)\) et ainsi :
\(\overrightarrow{u}\begin{pmatrix} 2 \\ 1\end{pmatrix}\).
\((d)\) est perpendiculaire à la droite \((AB)\) donc le vecteur \(\overrightarrow{AB}\) est un vecteur normal à \((d)\) et ainsi
\(\overrightarrow{n_2}\begin{pmatrix} 3 \\ -6\end{pmatrix}\).
Faire une figure, tracer un vecteur directeur de \((d)\) et un vecteur normal à \((d)\).
Question 4
Déterminer une équation de la droite \((d)\).
\( \begin{align*}M(x;y) \in (d) & \Leftrightarrow \overrightarrow{CM}.\overrightarrow{AB}= 0\\ &\Leftrightarrow 3(x -3) - 6(y - 3) = 0\\ & \Leftrightarrow x - 2y + 3 = 0 \end{align*}\)
Une équation de \((d)\)est donc : \( x - 2y + 3 = 0\)
On a un vecteur normal à \((d)\), il nous faut un point de cette droite.
Question 5
Déterminer les coordonnées du point d'intersection \(E\) des droites \((AB)\) et \((d)\).
Les coordonnées du point \(E\) sont solutions du système suivant :
\(x - 2y + 3 = 0 \Leftrightarrow x = 2y - 3 \Leftrightarrow x = 2y - 3 \Leftrightarrow x = - 1\\ 2x + y + 1 = 0 \Leftrightarrow 4y - 6 + y + 1 = 0 \Leftrightarrow 5y - 5 = 0 \Leftrightarrow y = 1\)
Il faut résoudre un système d'équations !
Penser à vérifier les solutions de ce système.
Penser aussi à vérifier sur le graphique les coordonnées trouvées pour le point \(E\).
Question 6
Déterminer l'aire du triangle \(ABC\). On pourra au préalable calculer les longueurs \(AB\) et \(CE\).
On a \(\overrightarrow{AB}\begin{pmatrix} 3 \\ -6\end{pmatrix}\) donc \(AB = \sqrt {45}\)
soit \( AB = 3\sqrt5\)
On a \(\overrightarrow{CE}\begin{pmatrix} -4 \\ -2\end{pmatrix}\) donc \(CE = \sqrt {20}\)
soit \( CE = 2\sqrt5\)
Ainsi :
\(A_{ABC} =\dfrac{1}{2} (AB\times CE)\)
\(A_{ABC} = \dfrac{1}{2}(3\sqrt{5} \times 2\sqrt{5})\) et donc
\(A_{ABC} = 15u^2\)
L'aire d'un triangle est \(\dfrac{base\times hauteur}{2}\)
Quelle hauteur et quelle base va t'on choisir ? Regarder la figure.
Si \(\overrightarrow{AB}\begin{pmatrix} a \\ b \end{pmatrix}\) alors sa norme est \(|\overrightarrow{AB}|= AB = \sqrt{a^2+b^2}\)