L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Soient \(\overrightarrow{u}\begin{pmatrix} 5 \\ 3\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} -2 \\ 1\end{pmatrix}\). Alors, \(\overrightarrow{u}.\overrightarrow{v}\) vaut :
$11$
$13$
$-7$
$-13$
Quel renseignement as-tu sur les vecteurs ? Leurs normes ? L'angle qu'ils forment ? Leurs coordonnées ?
Utilise alors la formule appropriée.
Attention aux erreurs de signes !
On te donne les coordonnées des vecteurs ; tu ne dois donc pas hésiter sur la formule à utiliser.
\(\overrightarrow{u}.\overrightarrow{v}=5\times (-2) +3\times 1\) donc \(\overrightarrow{u}.\overrightarrow{v}=-10 +3=-7\)
Question 2
Quelles sont la ou les propositions correctes ? Soient \(\overrightarrow{u}\begin{pmatrix} 1 \\ 4\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} -4 \\ 1\end{pmatrix}\).
\(\overrightarrow{u}.\overrightarrow{v}= 4\)
\(\overrightarrow{u}= 4\overrightarrow{v}\)
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont orthogonaux.
\(||\overrightarrow{u}||= ||\overrightarrow{v}| |\)
Que peut-on calculer lorsqu'on a les coordonnées de deux vecteurs ?
Calcule le produit scalaire de \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Calcule aussi la norme de chaque vecteur.
\(\overrightarrow{u}.\overrightarrow{v}= 0\) donc \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont orthogonaux (proposition 3)
Pour avoir \(\overrightarrow{u}=4\overrightarrow{v}\) il faudrait que \(\overrightarrow{u}\begin{pmatrix} 1 \\ 4\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} 4 \\ 16 \end{pmatrix}\)
\(||\overrightarrow{u}| |= \sqrt{(1^2+4^2)}\) soit \(||\overrightarrow{u}| |= \sqrt {17}\). De même \(||\overrightarrow{v}|| = \sqrt{(-4)^2+1^2}=\sqrt{17}\).
Question 3
Soient trois points distincts \(A\), \(B\) et \(C\) tels que \(AB = 4\), \(AC = 3\) et \(\widehat{BAC} = 30°\).
Alors \(\overrightarrow{AB}.\overrightarrow{AC}\) vaut :
\(-6 \times \sqrt 3 \)
$6$
\(6 \times \sqrt 3 \)
$0$
Quel renseignement as-tu sur les vecteurs ? Leurs normes ? L'angle qu'ils forment ? Leurs coordonnées ?
Utilise alors la formule appropriée.
On utilise la valeur exacte de \(\cos(30°)\) à savoir \(\frac{1}{2}\sqrt(3)\) et on obtient :
\(\overrightarrow{AB}.\overrightarrow{AC}= ||\overrightarrow{AB}||.||\overrightarrow{AC}||\times \cos(\widehat{BAC})\)
\(\overrightarrow{AB}.\overrightarrow{AC}= 12 \times \cos(30°)\)
\(\overrightarrow{AB}.\overrightarrow{AC}= 12 \times \frac{1}{2}\sqrt 3 \) soit une fois simplifiée :
\(\overrightarrow{AB}.\overrightarrow{AC}= 6 \times \sqrt 3 \)
Question 4
\(\overrightarrow{BC}.\overrightarrow{BA}= 14\)
\(\overrightarrow{BC}.\overrightarrow{BA}= 21\)
\(\cos( \widehat{ABC})= \dfrac{3}{7}\)
\(\cos( \widehat{ABC})= \dfrac{2}{3}\)
Quel renseignement as-tu sur les vecteurs ?
Avant d'utiliser la définition utilisant le projeté orthogonal, vérifie que tes vecteurs ont bien la même origine.
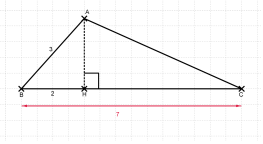
Ici, on projette le point \(A \) sur la droite \((BC)\).
L'angle \(\widehat{ABC} \) est le même que l'angle \(\widehat{ABH}\). On utilise ici la définition du cosinus vue en classe de 4e dans un triangle rectangle !
\(H\) étant le projeté orthogonal du point \(A\) sur la droite \((BC)\) on a :
\(\overrightarrow{BC}.\overrightarrow{BA}= \overrightarrow{BC}.\overrightarrow{BH}\)
Comme \(\overrightarrow{BC}\) et \(\overrightarrow{BH}\) sont colinéaires et de même sens alors :
\(\overrightarrow{BC}.\overrightarrow{BH} = BC \times BH\) soit \(\overrightarrow{BC}.\overrightarrow{BH} = 14\)
On peut aussi écrire : \(\overrightarrow{BC}.\overrightarrow{BA}=\overrightarrow{BC}.\overrightarrow{BH}\) soit
\(\overrightarrow{BC}.\overrightarrow{BA}= BC \times BH \times \cos(\widehat{HBC})\)
Et comme \(\widehat{HBC}=0°\) alors \( \cos(\widehat{HBC})= 1 \)
Dans le triangle \(ABH\) rectangle en \(H\) on a :
\(\cos( \widehat{ABH})=\cos( \widehat{ABC})= \frac{2}{3}\) (côté adjacent/hypoténuse)
Question 5
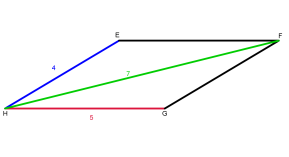
\(\overrightarrow{HE}.\overrightarrow{HG}= 4\)
\(\overrightarrow{HE}.\overrightarrow{HG}= 20\)
\(\cos( \widehat{EHG}) = \dfrac{1}{5}\)
\(\cos( \widehat{EGH}) = \dfrac{4}{7}\)
Ici pas de coordonnées ni de projeté orthogonal. Par contre tu connais la norme des vecteurs.
Il va aussi falloir trouver le cosinus de l'angle \(\widehat{EHG}\)
\(\overrightarrow{u}.\overrightarrow{v}= \dfrac{1}{2}(||\overrightarrow{u}+\overrightarrow{v}||^2-....)\) donc
\(\overrightarrow{HE}.\overrightarrow{HG}= \dfrac{1}{2}(||\overrightarrow{HE}+\overrightarrow{HG}||^2-....)\)
De plus \(\overrightarrow{HE} +\overrightarrow{ HG}=\overrightarrow{HF}\) d'après la règle du parallélogramme.
Maintenant que tu connais la valeur de \(\overrightarrow{HE}.\overrightarrow{HG}\), utilise une autre définition du produit scalaire pour trouver le cosinus de l'angle \(\widehat{EHG}\) en résolvant une équation.
\(\overrightarrow{HE}.\overrightarrow{HG}= \dfrac{1}{2}(||\overrightarrow{HE}+\overrightarrow{HG}||^2-||\overrightarrow{HE}||^2 -||\overrightarrow{HG}||^2)\)
\(\overrightarrow{HE}.\overrightarrow{HG}= \dfrac{1}{2}(||\overrightarrow{HF}||^2- ||\overrightarrow{HE}||^2 -||\overrightarrow{HG}||^2)\)
\(\overrightarrow{HE}.\overrightarrow{HG}= \dfrac{1}{2}(7^2-4^2-5^2)\) donc \(\overrightarrow{HE}.\overrightarrow{HG}= \dfrac{1}{2}\times 8 = 4\)
D'une autre part: \(\overrightarrow{HE}.\overrightarrow{HG}= ||\overrightarrow{HE}||.||\overrightarrow{HG}||^2. \cos( \widehat{EHG})\)
soit: \(\overrightarrow{HE}.\overrightarrow{HG}=20. \cos( \widehat{EHG})\)
D'autre part \(\overrightarrow{HE}.\overrightarrow{HG}= 4\)
Par conséquent: \(20 \cos( \widehat{EHG})=4 \Leftrightarrow \cos( \widehat{EHG}) = \dfrac{1}{5} \)