L'énoncé
Répondre aux questions suivantes. Le point $I$ est le milieu du segment $[AB]$
Question 1
Trouver la longueur $MI$.
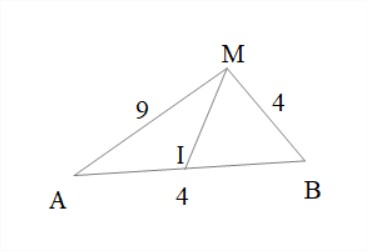
On va utiliser la formule de la médiane, soit encore :
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
donc $16+81=2MI^2+16$ ainsi $MI=\dfrac{\sqrt 81}{\sqrt 2}$.
On utilise la formule de la médiane :
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
Question 2
Trouver la longueur $MA$.
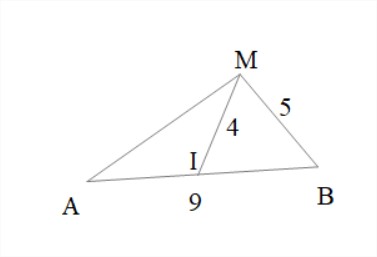
On va utiliser la formule de la médiane, soit encore :
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
donc $MA^2+25=32+81$ ainsi $MA=\sqrt {88}$.
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
Question 3
Soit $AB=5$, trouver tous les points tel que $MA^2+MB^2=37$.
On va donc utiliser la formule de la médiane, en plaçant un point $M$ mobile dans le plan.
Soit $2MI^2+\dfrac{25}{2}=37$ donc $MI=\dfrac{\sqrt{49}}{2}=\dfrac{7}{2}$.
Le point $M$ décrit alors le cercle de centre $I$, milieux de $AB$ et de rayon $MI$.
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
Question 4
Soit $AB=8$, trouver tous les points $M$ du plan tel que $MA^2+MB^2=47$.
On va donc utiliser la formule de la médiane, en plaçant un point $M$ mobile dans le plan.
Soit $2MI^2+\dfrac{64}{2}=47$ donc $MI=\sqrt{\dfrac{5}{2}}$.
Le point $M$ décrit alors le cercle de centre $I$, milieux de $AB$ et de rayon $MI$.
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
Question 5
Trouver la valeur de $AB$.
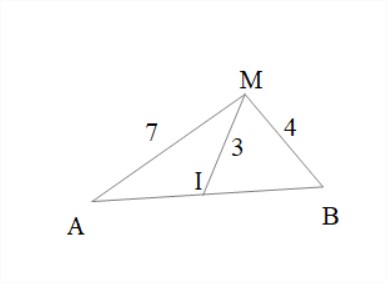
On va utiliser la formule de la médiane, soit encore :
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
donc $16+49=18+\dfrac{AB^2}{2}$
Ainsi $AB=\sqrt{94}$.
$MB^2+MA^2=2MI^2+\dfrac{AB^2}{2}$
