Transformation de ${MA}^2 + {MB}^2$. Formule de la médiane

Transformation de ${MA}^2 + {MB}^2$ à l'aide du milieu de $[AB]$ - Formule de la médiane

I) Théorème de la médiane : transformation de l'expression ${MA}^2 + {MB}^2$

Propriété : 

Soient deux points $A$ et $B$ et $I$ milieu de $[AB]$,

Pour tout point $M$, on a :

${MA}^2 + {MB}^2 = 2{MI}^2 + \dfrac{{AB}^2}{2}$

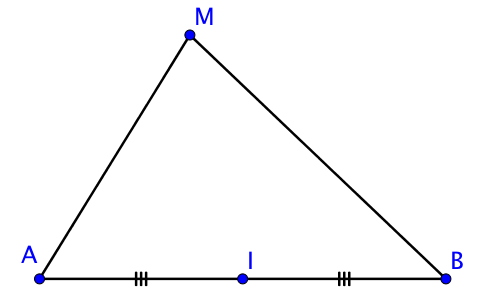
Cette formule s'appelle la formule de la médiane car elle fait intervenir $MI$ qui est la longueur de la médiane relative à $[AB]$. 

Rappels :

Le produit scalaire $\overrightarrow{MA} . \overrightarrow{MA}$ peut être calculé de différentes manières.

Il peut être calculé en considérant le produit de la norme de $\overrightarrow{MA}$ par la norme du projeté orthogonal de $\overrightarrow{MA}$ sur lui même, à savoir lui même.

Autrement dit,  $\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA = {MA}^2$, où $MA = \| \overrightarrow{MA} \|$.

On peut aussi utiliser la form