L'énoncé
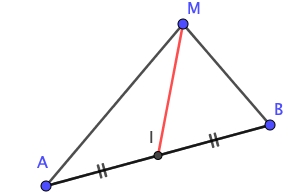
On considère un segment $[AB]$ de milieu $I$.
$M$ est un point quelconque du plan.
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle proposition est toujours vraie ?
$(MA)^2=\overrightarrow{MA}\cdot\overrightarrow{MA}$
$\overrightarrow{MA}\cdot\overrightarrow{MA}=0$
$\overrightarrow{MA}\cdot\overrightarrow{MA}=1$
Il s'agit de la définition du produit scalaire.
Question 2
Quelle est la bonne relation de Chasles ?
$\overrightarrow{IM}+\overrightarrow{IA}=\overrightarrow{MA}$
$\overrightarrow{MI}+\overrightarrow{IA}=\overrightarrow{MA}$
$\overrightarrow{IM}+\overrightarrow{AI}=\overrightarrow{MA}$
$\overrightarrow{IM}-\overrightarrow{AI}=\overrightarrow{MA}$
On insère le $I$ entre le $M$ et le $A$ et obtient la réponse $\overrightarrow{MI}+\overrightarrow{IA}$
Question 3
Que vaut $(\overrightarrow{MI}+\overrightarrow{IA})^2$ ?
$(MI)^2 -(IA)^2$
$(MI)^2-2\times \overrightarrow{MI}\cdot\overrightarrow{IA} +(IA)^2$
$(MI)^2+2\times \overrightarrow{MI}\cdot\overrightarrow{IA} +(IA)^2$
$(MI)^2 +(IA)^2$
On utilise les identités remarquables habituelles pour avoir la réponse.
Question 4
Soit $P$ un point du plan différent de $I$.
Que vaut $\overrightarrow{MP}\cdot(\overrightarrow{PA}+\overrightarrow{PB})$ ?
$\overrightarrow{MP}\cdot\overrightarrow{PA}+\overrightarrow{PB}$
$\overrightarrow{MP}\cdot\overrightarrow{PB}+\overrightarrow{PA}$
$\overrightarrow{MP}\cdot\overrightarrow{PA}+\overrightarrow{MP}\cdot\overrightarrow{PB}$
Le produit scalaire se développe comme une multiplication pour les réels. La réponse est donc :
$\overrightarrow{MP}\cdot\overrightarrow{PA}+\overrightarrow{MP}\cdot\overrightarrow{PB}$
Question 5
Quelle proposition est vraie ?
$(IA)^2=\dfrac{(AB)^2}{2}$
$(IA)^2=(IB)^2$
$(IA)^2=-(BI)^2$
$(AB)^2=\dfrac{(AI)^2}{4}$
Quand on met au carré le signe - disparait et une norme ne peut être négative.
Question 6
Quelle est la formule de la médiane ?
$(MA)^2+(MB)^2=MI +\dfrac{(AB)^2}{2}$
$(MA)^2+(MB)^2=2MI +\dfrac{(AB)^2}{2}$
$(MA)^2+(MB)^2=2(MI)^2 +\dfrac{(AB)^2}{4}$
$(MA)^2+(MB)^2=2(MI)^2 +\dfrac{(AB)^2}{2}$
Formule démontrée dans la vidéo.
Question 7
On considère un triangle $AMB$ avec $AB=2 cm$, $AM=4cm$ et $MB=6cm$.
Que vaut $MI$ ?
$2 cm$
$3 cm$
$4 cm$
$5 cm$
On utilisa la formule de la médiane $(MA)^2+(MB)^2=2(MI)^2 +\dfrac{(AB)^2}{2}$.
On a donc $2(MI)^2 = 16 +36 -4/2=50$
On a donc $(MI)^2=25$ soit $MI=5 cm$.
Question 8
On considère cette fois un triangle $ABM$ avec les valeurs suivantes $AB=6 cm$, $AM= 7 cm$ et $MB=5 cm$.
Que vaut $MI$ ?
$\sqrt{26}$
$\sqrt{27}$
$\sqrt{28}$
$\sqrt{29}$
On utilise encore la formule de la médiane
On a : $2(MI)^2=49+25-36/2=56$ soit
$MI=\sqrt{28}$.
Question 9
On considère un triangle $AMB$ tel que $(MA)^2+(MB)^2=40$ et $AB=4cm$.
Que vaut $MI$ ?
$5 cm$
$6 cm$
$7 cm$
$8 cm$
On utilise la formule de la médiane et $2(MI)^2=80-16/2=72$
On a donc $(MI)^2=36$ et donc $MI=6$
Question 10
Quel est l'ensemble des points $M$ du plan vérifiant $MI=6 cm$.
Un segment de longueur $6cm$.
Un disque de centre $I$ et de rayon $6cm$.
Un cercle de diamètre $6cm$ et de centre $I$.
Un cercle de rayon $6cm$ et de centre $I$.
L'ensemble des points $M$ est tel que $MI=6cm$ donc il s'agit d'un cercle de rayon $6 cm$ et de rayon $I$.
