Fiche de cours
Reconnaitre une équation de cercle, Déterminer centre et rayon
I) Les deux formes d'équation de cercle
1) Forme centre rayon
Soit $\mathcal{C}$ un cercle de centre $A(x_A;y_A)$ et de rayon $R$,
Soit $M(x; y)$ un point du plan,
$M$ appartient au cercle si et seulement si il est équidistant du centre.
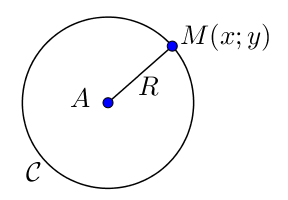
Ainsi, $M \in \mathcal{C} \iff AM = R \iff {AM}^2 = R^2$.
Calculons les coordonnées du vecteur $\overrightarrow{AM}$ :
$\overrightarrow{AM} \left ( \begin{array}{c} x - x_A \\ y - y_A \end{array} \right )$
Ainsi, $AM = \sqrt{(x - x_A)^2 + (y - y_A)^2}$ et donc ${AM}^2 = (x - x_A)^2 + (y - y_A)^2$.
En remplaçant dans l'équivalence initiale, on obtient :
$M \in \mathcal{C} \iff (x - x_A)^2 + (y - y_A)^2 = R^2$
Formule :
L'équation cartésienne du cercle centré en $A(x_A; y_A)$ de rayon $R$ est donnée par $(x - x_A)^2 + (y - y_A)^2 = R^2$.
Exemple :
On demande pour chaque équation de donner le centre et
