Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Déterminer les points d'intersections d'un cercle ou d'un parabole avec une droite parallèle à un axe
I) Points d'intersection d'une parabole $\mathcal{P}$ d'équation $p(x) = ax^2 + bx + c$ avec une droite $\mathcal{D}$
Remarque 1 :
Un point $M(x, y)$ appartient à la parabole $\mathcal{P}$ si et seulement si $y = p(x)$, c'est à dire que $y$ est l'image de $x$ par la fonction $p$.
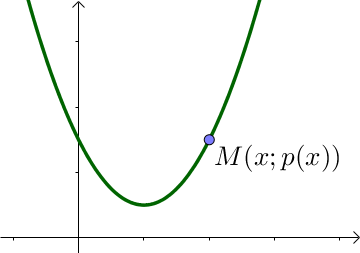
Remarque 2 :
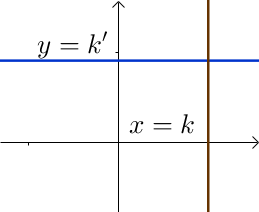
Une droite parallèle à l'axe des ordonnées a pour équation $x = k$, avec $k$ un réel.
Une droite parallèle à l'axe des abscisses a pour équation $y = k'$, avec $k'$ un réel.
a) Droite parallèle à l'axe des ordonnées d'équation $ x= k$
Comme il ne correspond à chaque $x$ une et une seule image par la fonct
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
