L'énoncé
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = x^2 + 3x + 1\).
Question 1
Soit \(a \in \mathbb{R}\) et \(h\) un réel strictement positif.
Montrer que \(\dfrac{f(a + h) -f(a)} { h} = h + 2a + 3\)
On a : \(f(a + h) = (a + h)^2 + 3(a + h) + 1 \) soit :
\(f(a + h) = a^2 + h^2 + 2ah + 3a + 3h + 1\)
\(f(a) = a^2 + 3a + 1\)
On a donc, pour \(h\) non nul :
\(\begin{align*}\dfrac{f(a + h) - f(a)} { h} &= \dfrac{h^2 + 2ah + 3h} {h} \\ &= h + 2a + 3 \end{align*}\)
Préciser que \(h\) ne peut être égal à \(0\) !
Question 2
En déduire \(f '(a)\) pour tout réel \(a\).
Plus \(h\) se rapproche de \(0\) plus \(h + 2a + 3\) se rapproche de \(2a + 3\).
On a donc \(\displaystyle \lim_{h \to0}\dfrac{f(a + h) f(a) }{ h} = 2a + 3\)
Par conséquent \(f\) est dérivable en \( a\) et pour tous réels \(a, f '(a) = 2a + 3\).
L'appliquer
Question 3
Tu connais \(f '(a)\) donc \(f '( - 1)\).
Question 4
Quel est le coefficient directeur de \(T\) ?
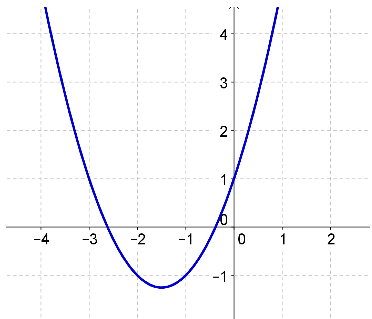
Question 5
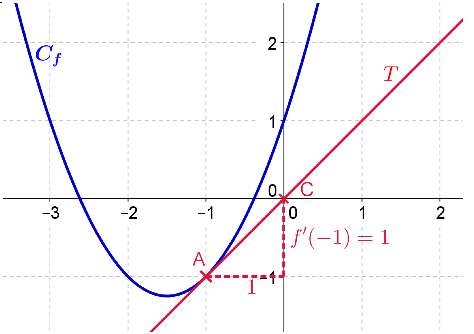
Déterminer l'équation de \(T\).
On a :
\(T : y = f '(-1) ( x + 1) + f(-1) \)
Avec \( f '(- 1) = 1\) et \(f( - 1) = - 1\)
Donc \(T : y = x\)
Appliquez la !
Question 6
Déterminer la position relative de \(C_f\) et de \(T\) et vérifier la cohérence du résultat sur le graphique.
Pour tous réels \(x, \ f(x) - x = x^2 + 2x + 1\)
On reconnaît une identité remarquable : \(f(x)- x = (x + 1)^2\)
Pour tous réels \(x, \ f(x) - x \geq 0\) donc \(f(x) \geq x \) et donc \(C_f\) est au-dessus de \(T\) sur \(\mathbb{R}\).
De plus l'équation \( f(x) - g(x) = 0\) ou encore \(f(x) = g(x)\) a une solution sur \(\mathbb{R}\).
Ainsi, \(C_f\) et \(T\) ont un point d'intersection sur \(\mathbb{R}\) (le point d'abscisse \(-1\)).
Sur le graphique on constate aussi que \(C_f\) est au-dessus de \(T\) sur \(\mathbb{R}\).
On note aussi que \(C_f\) et \(T\) n'ont qu'un unique point d'intersection : le point \(A\).
Chercher le signe de \(f(x) – (-2x + 5)\) sur \(\mathbb{R}\).
Comment obtenir le signe d'un polynôme du second degré ?