L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses
Tu as obtenu le score de
Question 1
La courbe \(C_f\) est celle d'une fonction \(f\). On a tracé les tangentes à \(C_f\) en \(a\) et en \(b\).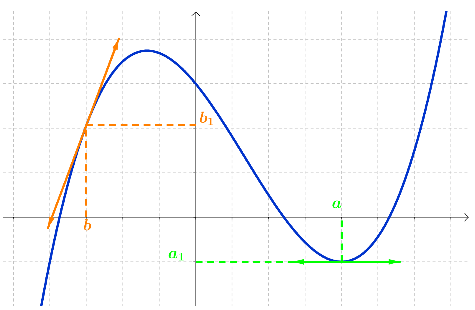
\(f '(a) = 0\)
\(f '(a) = a_1\)
\(f '(b) = - 2\)
\(f '(b) = b_1\)
Quelle est la différence entre \(f(a)\) et \(f '(a)\) ?
\(f '(a)\) est le coefficient directeur de la tangente à \(C_f\) en \(a\) idem pour \(f '(b)\).
Quel est le signe de \(f '(b)\) ?
La tangente à \(C_f\) en \(b\) a un coefficient directeur positif (fonction affine croissante) donc la proposition 3 est fausse.
Ce n'est pas \(f '(b)\) mais \(f(b)\) qui vaut \(b_1\) et de même \( f(a) = a_1\).
La tangente à \(C_f\) en \(a\) est horizontale ; son coefficient directeur est donc nul et \(f '(a) = 0\).
Question 2
La courbe \(C_f\) ci-dessous représente une fonction \(f\). La droite \((d)\) est la tangente à \(C_f\) en \(2\) et a pour équation \(y = 1,5x- 4\).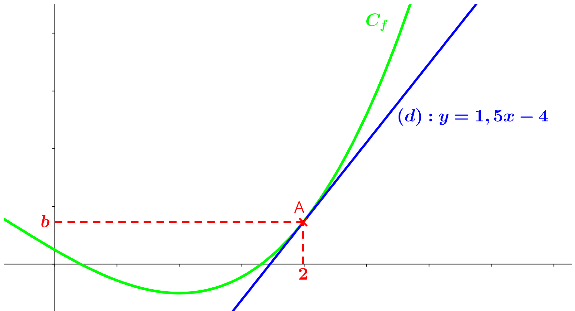
\(f(2) = b \) et \( f '(2) = 1,5\)
\(f(2) = 1,5 \) et \( f '(2) = b\)
\(f(2) = 2 \) et \( f '(2) = b\)
\(f(2) = b \) et \( f '(2) = 2\)
Quelles sont les coordonnées du point \(A\) ?
Que vaut alors \(f(2)\) ?
Que représente \(f '(2) \) sur la figure ?
\(A(2 ; b) \in C_f\) donc \(f(2) = b\).
\((d) : y = 1,5x – 4\) est tangente à \(C_f\) en \(2\) donc son coefficient directeur est le nombre dérivé de \(f\) en \(2\) et \(f '(2) = 1,5\).
Question 3
Soit \(f\) la fonction définie sur \(]0 ; +\infty[\) par \(f(x) = \dfrac{2}{x} + 5\) et telle que \(f '(1) = - 2\).
La tangente à \(C_f\) en \(1\) a pour équation réduite :
\(y = - 2x + 9 \)
\(y = - 2x + 7 \)
\(y = 7x -2 \)
\(y = 7x - 9 \)
Que représente \(f '(1)\) pour cette tangente ?
Quelles propositions peut-on alors éliminer ?
Quelle est l'équation de cette tangente ?
Effectuer les calculs…
Comme \(f '(1) = -2\) alors le coefficient directeur de la tangente est \(– 2\). On élimine donc les propositions 3 et 4.
La tangente a pour équation :
\(y = f '(1) (x – 1) + f(1) \) avec \( f '(1) = - 2\) et \(f(1) = \rfrac{2}{1} + 5 = 7\)
\((T) : y = - 2(x – 1) + 7\) soit \(y = - 2x + 9\)
Question 4
Soit \(h\) la fonction définie sur \(\mathbb{R}\) par \(h(x) = x^2 - 3\) et telle que \(h '(- 2) = - 4\). La tangente à \(C_h\) en \(-2\) a pour équation réduite :
\(y = - 4x + 15\)
\(y = - 4x -7\)
\(y = 7x- 4\)
\(y = - 4x+1\)
Que représente \(h '(-2)\) pour cette tangente ?
Quelle proposition peux-tu alors éliminer ?
Quelle est l'équation de cette tangente ?
Comme \(h '( -2) = -4\) alors le coefficient directeur de la tangente est \(– 4\). On élimine donc la proposition 3.
La tangente a pour équation :
\(y = h '( -2)(x – (- 2)) + h(-2)\) avec \( h '( -2) = - 4 \) et \(h(-2) = (- 2)^2 - 3 = 1\)
\((T) : y = - 4(x + 2) + 1\) soit \(y = - 4x - 7\)
Question 5
On a représenté ci-dessous la courbe d'une fonction \(f\) ainsi que les tangentes en \(6\) points. Donner les affirmations correctes :
L'équation \(f(x) = 0\) a 6 solutions.
L'équation \(f'(x) = 0\) a 6 solutions.
\(C_f\) admet 6 tangentes horizontales donc l'équation \(f '(x) = 0\) a 6 solutions.
\(f '(1) < 0\)
La tangente en 1 est associée à une fonction affine décroissante et donc de coefficient directeur négatif. Son coefficient directeur est \(f '(1)\) et donc \(f '(1) < 0 \).
\(f '(5) < 0\)
La tangente en 5 est associée à une fonction affine croissante et donc de coefficient directeur positif. Son coefficient directeur est \(f '(5)\) et donc \(f '(5) > 0\).
Ne pas confondre \(f(x) = 0\) et \(f '(x) = 0\).
Où \(C_f\) coupe-t-elle l'axe des abscisses ? A quoi ces valeurs correspondent-elles ?
Quel est le coefficient directeur de la tangente lorsqu'elle est horizontale ?
La tangente en \(1\) n'est pas tracée mais si elle l'était serait-elle associée à une fonction affine croissante ou décroissante ? Quel serait alors le signe de son coefficient directeur ?
\(C_f \) ne coupe pas l'axe des abscisses donc l'équation \(f(x) = 0\) n'a aucune solution.
\(C_f\) admet 6 tangentes horizontales donc l'équation \(f '(x) = 0\) a 6 solutions.
La tangente en 1 est associée à une fonction affine décroissante et donc de coefficient directeur négatif. Son coefficient directeur est \(f '(1)\) et donc \(f '(1) < 0 \).
La tangente en 5 est associée à une fonction affine croissante et donc de coefficient directeur positif. Son coefficient directeur est \(f '(5)\) et donc \(f '(5) > 0\).

\(C_f \) ne coupe pas l'axe des abscisses donc l'équation \(f(x) = 0\) n'a aucune solution.