L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
On a tracé la courbe d'une fonction \(h\).
\(h'(-3,5) = \frac{3}{5}\)
\(h'(-3,5) = \frac{5}{3}\)
\(h'(-2) = -2\)
\(h'(-2) = 1,2\)
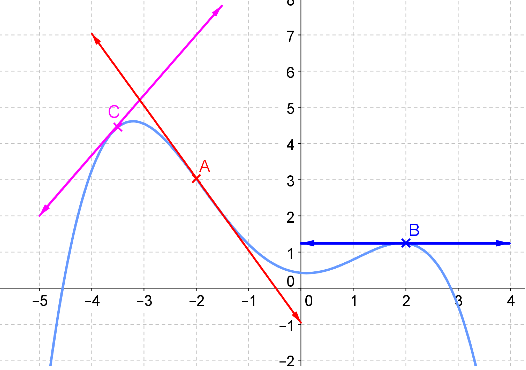
Graphiquement \(h'(a)\) est le coefficient directeur de la tangente à \(C_h\) au point d'abscisse \(a\).
Lis chaque coefficient directeur
Lorsque la tangente est horizontale, que vaut le coefficient directeur ?
La tangente à \(C_h\) en \(C\) a pour coefficient directeur \( \frac{5}{3}\) donc \(h'(-3,5) = \frac{5}{3}\).
La tangente à \(C_h\) en \(A\) a pour coefficient directeur \( - 2\) donc \(h'(- 2) = - 2\).
La tangente à \(C_h\) en \(B\) est horizontale donc \(h'(2) = 0\).
Question 2
Soit \(f\) une fonction définie sur \(\mathbb{R}\) telle que \(f(5) = 2, \ f(2)=5, \ f'(5) = - 1\) et \(f(-1) = 5\). La tangente \(T\) à \(C_f\) en \(x = 5\) a pour équation :
\(y= - x + 7\)
\(y= 5x -20\)
\(y= -x +2\)
\(y= 5x +5\)
Quel est le coefficient directeur de la tangente à \(C_f\) en \(x = 5\) ?
Quelles propositions peux-tu alors éliminer ?
Quelle est l’équation de la tangente à \(C_f\) en \(x = a\) ? Que vaut \(a\) ici ?
Cherche alors l’équation de la tangente.
Le coefficient directeur de la tangente à \(C_f\) en \(x = 5\) est \(f ‘(5) = - 1\). On élimine donc les propositions 2 et 4.
\(T\) a pour équation : \(y = f ‘(a)(x – a) + f(a) \) avec ici \(a = 5\).
\(T : y = -(x – 5) + f(5)\) soit \( y = - x + 7 \).
Question 3
Sachant que \(f(3) = 1\) et que \(f '(3) = 2\) donner, parmi les quatre droites tracées ci-dessous, celle qui représente la tangente à \(C_f\) en \(3\).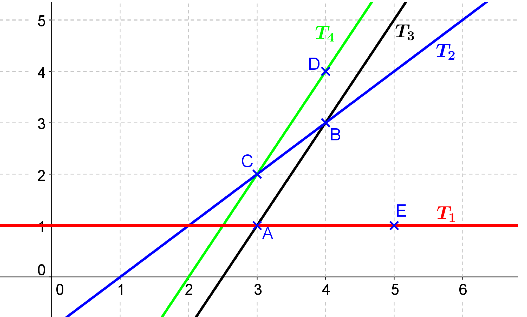
\(T_1\)
\(T_2\)
\(T_3\)
\(T_4\)
De \(f(3) = 1\) tu peux déduire les coordonnées d’un point de \(C_f\).
De \(f ‘(3) = 2\) tu peux déduire le coefficient directeur de la tangente cherchée.
\(f(3) = 1\) donc le point \( A(3 ; 1)\) appartient à \(C_f\).
\(f’( 3 )= 2\) on cherche donc une tangente de coefficient directeur 2.
Question 4
On a tracé ci-dessous la courbe représentative dune fonction et certaines de ses tangentes.
L’équation \(f ‘(x) = 0\) a pour ensemble solution \(S = \{ -0,25 ; 1,5\}\).
L’équation \(f ‘(x) = 0\) a pour ensemble solution \(S = \{ 0,5;3\}\).
La tangente à \(C_f\) en \(x = 0\) a pour équation \(y = - 4,5x - 9\).
\( \displaystyle\lim_{h\to0} \dfrac{f( h) -(-1,5)}{h} = -9\)
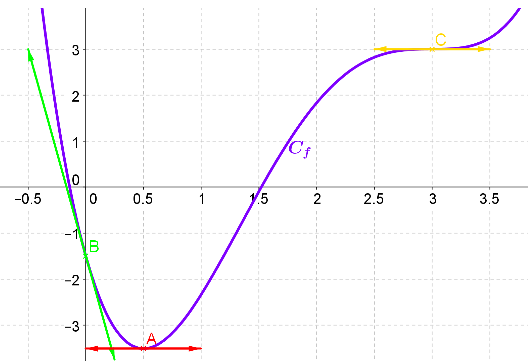
Comment lire graphiquement le nombre dérivé ? Et lorsqu’il vaut $0$ ?
Écris l’équation de la tangente à \(C_f\) en \(x = 0\).
Que représente \(\displaystyle\lim_{h\to0} \dfrac{f(a+h) – f(a)}{h}\) si elle existe ? Lire graphiquement.
\(C_f\) a 2 tangentes horizontales ; en \(0,5\) et \(3\).
Par conséquent, \(f '(0,5) = f '(3) = 0\) et l’équation \(f '(x) = 0\) a pour ensemble solutions :
\(S = \{0,5; 3\}\).
La tangente \(T\) à \(C_f\) en \(x = 0\) a pour équation : \(y = f '(0)(x-0) + f(0) \).
Or, \(f '(0) = - 9\) et \(f(0) = - 1,5\) donc l’équation de \( T\) est :
\(y = - 9x – 1,5\).
\( \lim_{h\to0} \large\frac{f(h)-( – 1,5)}{h-0}\) si elle existe est égale à \( f '(0)\) ; c’est donc le coefficient directeur de la tangente à \(C_f\) en \(0\).
Graphiquement on a \(f'(0) = -9\).
Question 5
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = x^2 + x + 4\) et \(T\) la tangente à \(C_f\) en \(x = 1\) dont léquation est \(y = 3x + 3.\)
\(C_f\) est au-dessus de \(T\) sur \(\mathbb{R}\).
\(C_f\) est au-dessous de \(T\) sur \(\mathbb{R}\).
\(C_f\) et \(T\) ont un unique point d’intersection sur \(\mathbb{R}\).
\(C_f\) et \(T\) ont deux points d’intersection sur \(\mathbb{R}\).
Quelle est la méthode pour déterminer la position relative de deux courbes ?
Calcule \(f(x) – (3x + 3)\) et cherches-en le signe sur \(\mathbb{R}\).
Comment obtenir le signe d'un polynôme du second degré ?
Pour déterminer la position relative de deux courbes sur un intervalle \(I\), on calcule \(f(x) – g(x)\) puis on en étudie le signe sur \(I\).
Pour déterminer les points d'intersection de deux courbes sur un intervalle \(I\), on résout l'équation \( f(x) = g(x) \) sur \(I\).
Pour tous réels \(x, \ f(x) – (3x + 3) = x^2 - 2x + 1\)
Le discriminant de ce polynôme vaut \(\Delta = 0 \) et donc \(x^2 + x + 1\) est du signe de \(a =1\) soit positif sur \(\mathbb{R}\).
Ill admet une racine double : \(x_1 = 1\). On a donc :
Pour tous réels \(x, \ f(x) – (3x + 3) \geq 0\) donc \(f(x) \geq (3x + 3)\)
On en conclut que \(C_f\) est au-dessus de \(T\) sur \(\mathbb{R}\) .
De plus l'équation \(f(x) - g(x) = 0\) ou encore \(f(x) = g(x)\) a une solution sur \(\mathbb{R}\)
conclusion : \(C_f\) et \(T\) ont un point d'intersection sur \(\mathbb{R}\) (le point d'abscisse 1).