L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
La fonction \(f\) définie par \(f(x) = \sqrt{ x^2 - 4x- 5}\) a pour ensemble de définition :
\( D_f=[0 ; +\infty[\)
\(D_f=[-1;-5]\)
\(D_f=] –\infty; -1 ] \cup [5 ; +\infty[\)
\(D_f=[5 ; +\infty[\)
On peut tracer la courbe sur ta calculatrice pour conjecturer son ensemble de définition.
\(\sqrt{ x}\) est définie que pour \(x \geq 0\) et \(\sqrt{x^2 – 4x – 5}\) n'est définie que pour \(x^2 – 4x – 5\geq 0\)
\(x^2 – 4x – 5\geq 0\) est un polynôme du second degré; comment trouver son signe ?
Pour tout réel x : \(x^2 – 4x – 5 = (x – 5)(x + 1)\) en développant l'expression \((x – 5)(x + 1)\).
Détermine alors son signe grâce à un tableau de signes (classe de 2nde).
\(f(x)\) est définie si et seulement si \( x^2 – 4x – 5\geq0\).
Soit \(\Delta\) le discriminant de ce polynôme alors,
\(\Delta = b^2 – 4ac\) avec \(a= 1\), \(b = - 4\) et \(c = - 5 \)
On a donc \(\Delta = 36\)
Ainsi \(x^2 – 4x – 5\) admet donc deux racines : \( x_1 = \frac{- b – \sqrt{\Delta}}{2a} = - 1\) et \(x_2 = \frac{- b + \sqrt{\Delta}}{2a} =5 \)
Ainsi, \( x^2 – 4x – 5 \geq 0\) pour \(x \in ] –\infty; -1 ] \cup [5 ; +\infty[\)
Question 2
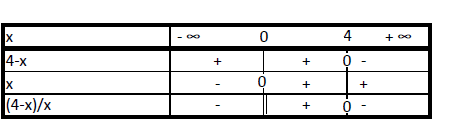
La fonction \(f\) définie par \(f(x) =\sqrt{\dfrac{{4-x}}{x}} \) a pour ensemble de définition :
\( D_f=]0 ; +\infty[\)
\(D_f=]0 ; 4]\)
\(D_f=] –\infty; 0 ] \cup [4 ; +\infty[\)
\(D_f= [0 ; 4]\)
Tu peux tracer la courbe sur ta calculatrice pour conjecturer son ensemble de définition.
\(f(x) = \sqrt{\dfrac{{4-x}}{x}} \) n'est définie que pour \(\dfrac{4-x}{x} \geq0 \) et \(x\) non nul.
Détermine alors son signe grâce à un tableau de signes (classe de 2nde). Attention à la ou aux valeur(s) interdite(s).
\(f(x)\) est définie si et seulement si \(\dfrac{4-x}{x} \geq0 \) et \(x\) non nul.
Donc \(D_f = ]0;4 ]\)
Question 3
Soit \(x\) un réel tel que \(4 \leq x\leq 16\). Alors \(-\dfrac{1}{2}\sqrt x + 3\) appartient à :
\( [1 ; 2]\)
\( [4 ; 5]\)
\( [0 ; +\infty[\)
\([-3.5;-2.5]\)
Encadrez déjà \(\sqrt{x}\).
Puis \(\dfrac{1}{2}\sqrt x \).
Et enfin \(-\dfrac{1}{2}\sqrt x + 3\) et attention aux éventuels changements de sens de l'inéquation !
On a : \(4 \leq x\leq 16\).
Comme la fonction racine carrée est croissante sur \( [4 ; 16]\) on a alors :
\(\sqrt 4 \leq \sqrt x\leq \sqrt 16\) soit :
\(2 \leq \sqrt x\leq 4\)
Ainsi : \(-\frac{1}{2}\times 2 \geq -\frac{1}{2}\times\sqrt x \geq -\frac{1}{2} \times4\) ( attention : \( -\frac{1}{2} < 0\) donc on change le sens de l'inégalité !)
Soit, \(-1 \geq -\frac{1}{2}\sqrt x \geq -2\) ou encore :
\(-2 \leq -\frac{1}{2}\sqrt x \leq -1\)
Finalement en ajoutant \(3\) :
\(1 \leq -\frac{1}{2}\sqrt x +3\leq 2\)
Et ainsi on en déduit que \(-\frac{1}{2}\sqrt x + 3\) appartient à l'intervalle \( [1 ; 2]\).
Question 4
La fonction \(f\) définie par \(f(x) =2\sqrt{x} +4\) alors :
\(f\) est décroissante sur \( [0 ; +\infty[\)
\(f\) est croissante sur \( [0 ; +\infty[\)
\(f\) est croissante sur \( \left[-\dfrac{1}{2} ; +\infty\right[\)
\(f\) est décroissante sur \( \left]-\infty;\dfrac{1}{2}\right]\)
On peut déjà supprimer deux propositions en cherchant \(\mathscr{D_f}\) le domaine de définition de \(f\) ?
Comparer alors \(f(a)\) et \(f(b)\) sachant que \(a\) et \(b\) sont deux réels de \(\mathscr{D_f}\) tels que \(a < b\)
\(f(x)\) est défini pour \(x \geq 0 \) donc sur \(\mathscr{D_f}= [0 ; +\infty[\)
Soient \(a\) et \(b\) deux réels de \(\mathscr{D_f}\) tels que : \(0 \leq a < b\) alors :
\(0 \leq \sqrt a< \sqrt b \) car la fonction racine carré est croissante sur \([0 ; +\infty[\)
Donc, \(0 \leq 2\sqrt a< 2\sqrt b \)
Ainsi, \(4 \leq 2\sqrt a + 4 < 2\sqrt b + 4 \)
Soit, \(4 \leq f(a) < f(b)\)
En conclusion, pour \(a\) et \(b\) deux réels de \(\mathscr{D_f}\) tels que \(a < b\) on a \(f(a) < f(b)\). \(f\) est donc croissante sur \(\mathscr{D_f}\).
Question 5
L'expression \(A(x) = \sqrt{x+1} -2\) définie sur \(]-1; +\infty [\) peut également s'écrire sous la forme :
\(A(x) = \dfrac{3}{\sqrt{x+1} + 2}\)
\(A(x) = \dfrac{2x + 3}{\sqrt{x+1} + 2}\)
\(A(x) = \dfrac{x – 3}{\sqrt{x+1} - 2}\)
\(A(x) = \dfrac{x – 3}{\sqrt{x+1} + 2}\)
Quelle est la quantité conjuguée de \( \sqrt{x+1} – 2\)
C'est \( \sqrt{x+1} + 2\)
\(A(x)\) est un quotient. Son numérateur vaut \(\sqrt{x+1} - 2\) mais quel est son dénominateur ?
C'est 1 !
Multiplie alors le numérateur et le dénominateur de \(A(x)\) par la quantité conjuguée de \( \sqrt{x+1} - 2\)
\(A(x) = \sqrt{x+1} + 2\) donc :
\(A(x) =\large \frac{(\sqrt{x+1} - 2)(\sqrt{x+1} + 2)}{\sqrt{x+1} + 2}\) ( Le dénominateur est strictement positif)
\(A(x) = \large\frac{\sqrt{x+1}^2 - 2^2}{\sqrt{x+1} + 2}\)
\(A(x) =\large \frac{x + 1 – 4}{\sqrt{x+1} + 2}\)
\(A(x) = \large\frac{x – 3}{\sqrt{x+1} + 2}\)