Une entreprise de menuiserie réalise des découpes dans des plaques rectangulaires de bois.

Dans un repère orthonormé d’unité 30 cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe $C_f$ représentative de la fonction $f$ définie sur l’intervalle $[−1; 2]$ par :

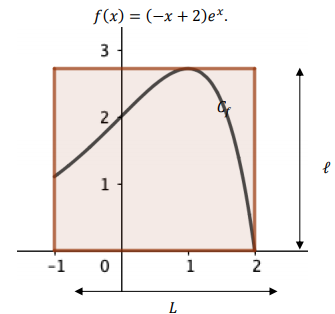
Le bord supérieur de la plaque rectangulaire est tangent à la courbe $C_f$. On nomme $L$ la longueur de la plaque rectangulaire et $l$ sa largeur.

1. On note $f'$ la fonction dérivée de $f$.

     a. Montrer que pour tout réel $x$ de l’intervalle $[−1; 2]$, $f'(x)=(-x+1)e^x$ .

     b. En déduire le tableau de variations de la fonction $f$ sur $[−1; 2]$.

2. La longueur $L$ de la plaque rectangulaire est de 90 cm. Trouver sa largeur $l$ exacte en cm.