L'énoncé
Cocher la bonne réponse.
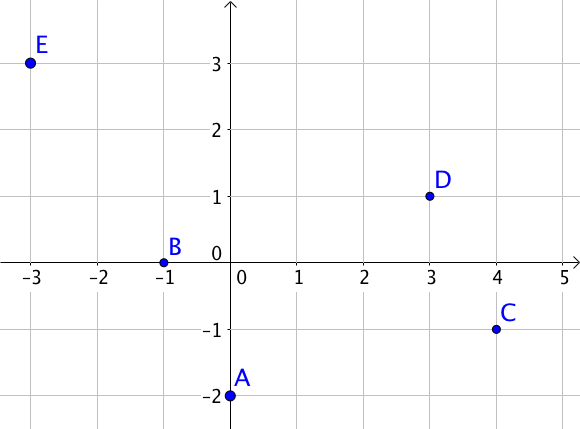
On utilisera le repère suivant dans la suite de l'exercice :
Tu as obtenu le score de
Question 1
Quelles sont les coordonnées du point $A$ ?

$A(-2;0)$
$A(0;-2)$
$A(0; 2)$
Le point $A$ appartient à l'axe des ordonnées, son abscisse vaut donc 0.
En outre, on doit se déplacer de 2 unités vers le bas pour atteindre $A$.
Son ordonnée est donc -2.
Ainsi, $A(0;-2)$
Question 2
Quelles sont les coordonnées du point $B$ ?

$B(0; -1)$
$B(1; 0)$
$B(-1; 0)$
Le point $B$ appartient à l'axe des abscisses, son ordonnée est donc nulle !
En outre, il faut parcourir une unité vers la gauche pour atteindre $B$.
Son abscisse vaut donc $-1$.
Ainsi, les coordonnées de $B$ sont $(-1; 0)$.
Question 3
Quelles sont les coordonnées du point $C$ ?

$C(4; -1)$
$C(4; 1)$
$C(-1; 4)$
Pour atteindre le point $C$, on doit parcourir quatre unités vers la droite selon l'axe des abscisses : l'abscisse du point $C$ est donc 4.
On doit ensuite descendre d'une unité vers le bas selon l'axe des ordonnées, l'ordonnée est donc de $-1$.
Ainsi les coordonnées du point $C$ sont $(4; -1)$.
Question 4
Quelles sont les coordonnées du point $D$ ?

$D(3; 1)$
$D(1; 3)$
$D(-1; 3)$
Lorsque l'on trace des droites perpendiculaires aux axes des abscisses puis des ordonnées passant par $D$, on coupe l'axe des abscisses au point 3 et l'axe des ordonnées au point 1.
Ainsi, $D(3; 1)$.
Question 5
Quelles sont les coordonnées du point $E$ ?

$E(3; 3)$
$E(-3; 3)$
$E(3; -3)$
Lorsque l'on trace des droites perpendiculaires aux axes des abscisses puis des ordonnées passant par $E$, on coupe l'axe des abscisses au point -3 et l'axe des ordonnées au point 3.
Ainsi, $E(-3; 3)$.
