Cours Triangles semblables et égaux
lesbonsprofs.com
Image
Cours Triangles semblables et égaux
1
Video Triangles semblables
2
Exercice QCM - Triangles semblables
3
Video Triangles égaux
4
Exercice QCM - Triangles égaux
5
Exercice Exercice - Transformations
QCM
  • 1
  • 2
  • 3
  • 4
  • 5

L'énoncé

Trouver la ou les bonnes réponses.

Tu as obtenu le score de

Question 1

Deux triangles sont semblables…

lorsque leurs côtés sont de même longueur deux à deux.

Non, ça c'est la définition des triangles égaux ou superposables.

lorsqu'ils ont au moins un angle de même mesure.

Non, cela ne suffit pas.

lorsqu'ils ont les mêmes angles deux à deux.

Deux triangles sont semblables lorsqu'ils ont les mêmes angles deux à deux. On ne parle pas des longueurs des côtés, il peut donc y avoir un agrandissement ou une réduction de la figure.

Question 2

Trouver le ou les triangles semblables au triangle bleu $ABC$.

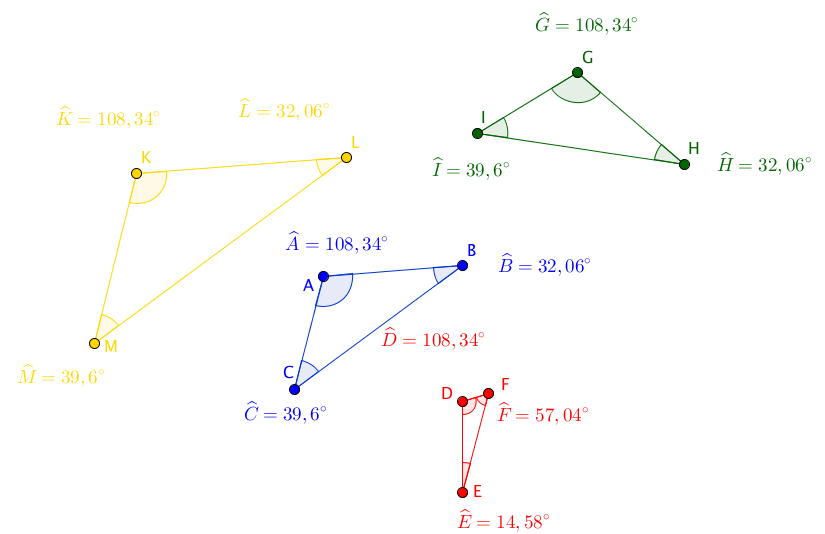
d92a5e5f990c5a53f654ed7646ad9bdc17899974.png

Le triangle rouge $DEF$
Non les angles ne sont pas égaux à ceux du triangle bleu.
Le triangle vert $GHI$.
Le triangle jaune $KLM$.

Question 3

Quel est la propriété des triangles semblables ?

Si deux triangles ont leurs côtés respectivement proportionnels alors ils sont semblables.
Si deux triangles ont deux côtés de même longueur compris entre deux angles respectivement égaux alors ces triangles sont semblables.
Non, dans ce cas les triangles sont égaux !
Si deux triangles ont deux angles égaux formés par des côtés respectivement égaux alors ces triangles sont semblables.
Non, dans ce cas les triangles sont égaux !

Question 4

Ci-après, deux triangles $ABC$ et $DEF$. 

Quelle est la condition, d'après les informations données, pour que ces deux triangles soient semblables ?

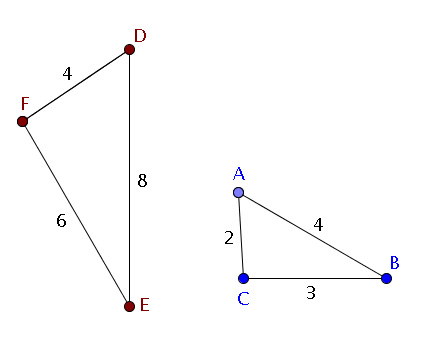
097688da8717e933d8b93defbd43a5db2af43b39.jpg

Il faut que le total des côtés pour chaque triangle soit le même.
Il faut que leurs côtés soient respectivement proportionnels.
On ne peut pas savoir, il faut calculer les angles.
On applique ici la propriété des triangles semblables.
Il faut que le rapport de proportionnalité entre les côtés soit respectivement le même. C'est-à-dire qu'il faut que : $\dfrac{DE}{AB} = \dfrac{FD}{CA} = \dfrac{FE}{CB}$

Question 5

Ces deux triangles sont-ils semblables ?

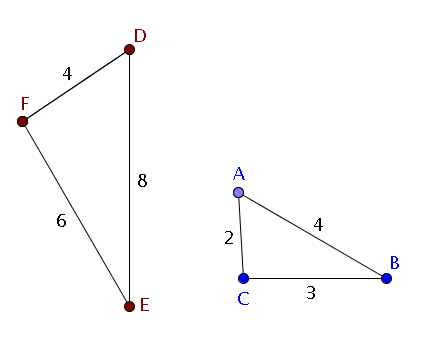
296012ec3782469c5b97791e7068467214f5b1c0.jpg

Oui.

Non.

Pour que ces triangles soient semblables, il faut que : $\dfrac{DE}{AB} = \dfrac{FD}{CA} = \dfrac{FE}{CB}$

Il faut que : $\dfrac{DE}{AB} = \dfrac{FD}{CA} = \dfrac{FE}{CB}$

$\dfrac{DE}{AB} = \dfrac{8}{4} = 2$

$ \dfrac{FD}{CA} = \dfrac{4}{2} = 2$

$\dfrac{FE}{CB} = \dfrac{6}{3} = 2$

 

Le rapport de proportionnalité est toujours $2$. Ces triangles sont donc semblables.