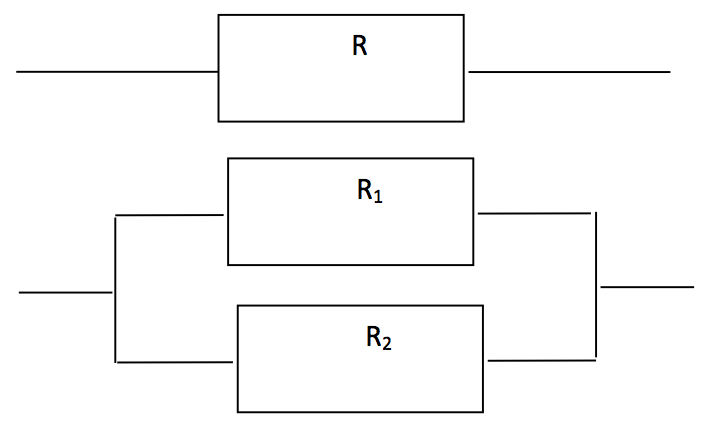
En électricité, pour calculer la résistance $R$ d’un dipôle ohmique équivalent à deux dipôles ohmiques de résistances respectives $R_1$ et $R_2$ montés en dérivation, (illustré sur le schéma ci-contre), on utilise la formule :
$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$
1) Calculer $R$ pour :
a) $R_1 = 9$ ohms et $R_2 = 8$ ohms
b) $R_1 = R_2 = 400$ ohms
2) On ne dispose que de dipôles ohmiques de résistance 1 000 ohms. Quel montage doit-on réaliser pour obtenir l’équivalent d’un dipôle ohmique de résistance 500 ohms ? d’un dipôle ohmique de résistance 250 ohms ?
1) $\dfrac{1}{R} = \dfrac {1}{R_1} + \dfrac{1}{R_2}$
a) $\dfrac{1}{R} = \dfrac{1}{9} + \dfrac{1}{8}$
$\dfrac{1}{R} = \dfrac{9+8}{72} = \dfrac{17}{72}$ donc $\boxed{R = \dfrac{72}{17} \, ohms}$
b) $\dfrac{1}{R} = \dfrac{1}{400} + \dfrac{1}{400} = \dfrac{2}{400} = \dfrac{1}{200}$ donc $R = 200 \, ohms$.
2) On ne dispose que de dipôles ohmiques de résistance 1 000 ohms.
On remarque que si l’on monte 2 dipôles ohmiques de résistance 1 000 ohms en dérivation on obtient :
$\dfrac{1}{R} = \dfrac{1}{1000} + \dfrac{1}{1000} = \dfrac{2}{1000} = \dfrac{1}{500}$, soit :
$R = 500\, ohms$.
Si l’on monte 4 dipôles ohmiques de résistance 1 000 ohms en dérivation on obtient :
$\dfrac{1}{R} = \dfrac{1}{1000} +\dfrac{1}{1000} +\dfrac{1}{1000}+\dfrac{1}{1000}$
$\dfrac{1}{R} = \dfrac{4}{1000} = \dfrac{1}{250}$, soit :
$R = 250 \, ohms$.
