L'énoncé
Dans la figure ci-dessous :
\(ABCD\) est un carré de côté \(9\) cm.
Les segments de même longueur sont codés.
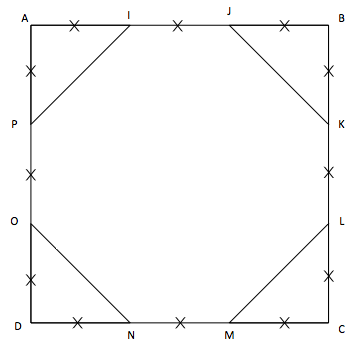
Question 1
Calculez la valeur exacte de \(JK\).
\(ABCD\) est un carré donc l'angle \(\widehat{JKB}\) est droit.
Par conséquent, le triangle \(JKB\) est un rectangle en \(B\).
D'après le théorème de Pythagore :
\(JK^2 = JB^2 + BK^2\)
Or le côté \([AB]\) mesure \(9\) cm et il divisé en trois parties égales d'après le codage de la figure.
On en déduit facilement que \(JB = BK = 3\) cm
On a donc :
\(JK^2 = 3^2 + 3^2\)
\(JK^2 = 9 + 9\)
\(JK^2 = 18\)
Doù \(JK = \sqrt{18} = 3 \sqrt{2}\)
\([JK]\) est l’hypoténuse du triangle \(JKB\).
Triangle dont on sait les dimensions puisque \(ABCD\) est un carré.
Triangle dont on connait déjà les longueurs de deux côtés
Théorème de Pythagore bien sûr !
Question 2
L'octogone \(IJKLMNOP\) est-il un octogone régulier ?
Vous venez de calculer dans la question 1 que \( JK = 3 \sqrt{2}\) cm.
De plus, on sait que \(IJ = 3\) cm.
Or vous savez qu'un polygone régulier est un polygone qui a tous ses côtés de même longueur et tous ses angles de même mesure.
Ce n'est pas le cas de \(IJKLMNOP\), puisque \(JK \neq IJ\).
Donc, \(IJKLMNOP\) n'est pas un octogone régulier.
Un polygone régulier est un polygone qui a tous ses côtés de même longueur et tous ses angles de même mesure.
Or ici, combien mesure \([JK]\) que vous venez de calculer?
Et \([IJ]\) ?
Question 3
Calculer l'aire du triangle \(JKB\).
Pour calculer l'aire dun triangle, on utilise la formule : Aire du triangle = \(\dfrac{base \times hauteur}{2}\)
Mais le triangle \(JKB\) est rectangle en \(B\). Ce qui donne :
Aire du triangle \( JKB = \dfrac{JB \times BK}{2} = \dfrac{3 \times 3}{2} = \dfrac{9}{2} = 4,5\) cm2.
Souvenez-vous que le triangle \(JKB\) est un triangle rectangle.
Aire du triangle = \(\dfrac{base \times hauteur}{2}\)
Mais dans un triangle rectangle, vous pouvez choisir de prendre les deux « petits côtés » comme base et hauteur.
Ce qui donne : Aire du triangle \( JKB = \dfrac{JB \times BK}{2}\)
Question 4
Sachant que Aire \( JKB = 4,5\) cm2,
Calculez l'aire de l'octogone \(IJKLMNOP\).
Il est clair que les quatre triangles \(JKB\), \(LCM\), \(ODN\) et \(AIP\) ont la même aire.
Aire \(JKB\) = Aire \(LCM\) = Aire \(ODN\) = Aire \(AIP\) = \(4,5\) cm2
Or ces quatre triangles sont dans le carré \(ABCD\) et on a donc :
Aire \(IJKLMNOP\) = Aire \(ABCD - 4 \times \) Aire \(JKB\)
Aire \(IJKLMNOP = 9^2 - 4 \times 4,5\)
Aire \(IJKLMNOP = 81 - 18\)
Aire \(IJKLMNOP = 63 \) cm²
Non, on ne vous demande pas de connaître la formule de l’aire d’un octogone ! Il y a un autre moyen.
Aire \(JKB\) = Aire \(LCM\) = Aire \(ODN\) = Aire \(AIP\) = \(4,5\) cm2
Et ces quatre triangles sont dans le carré \(ABCD\) …
Aire \(IJKLMNOP\) = Aire \(ABCD - 4 \times \) Aire \(JKB\)
Question 5
Les diagonales du carré \(ABCD\) se coupent en \(S\).
On trace le disque de centre \(S\) et de diamètre \(9\) cm.
On considère le point \(H\) le milieu du segment \([AB]\).
Le point \(I\) appartient-il au disque ?

On considère \(H\) le milieu du segment \([AB]\).
Le disque est de diamètre \(9\) cm, son rayon est donc égal à \(4,5\) cm.
\(SH\) est égal à \(4,5\) cm donc \(H\) est sur le cercle de centre \(S\) et de rayon \(4,5\) cm.
\(SHI\) est donc un triangle rectangle dont l'hypoténuse est le segment \([SI]\).
\([SI]\) est donc le plus grand côté, sa longueur est donc supérieure à \(4,5\) cm.
Par conséquent puisque \(SI\) est supérieur au rayon du disque.
Nous en déduisons que \(I\) n'appartient pas au disque.
Le disque est de diamètre \(9\) cm, son rayon est donc égal à \(4,5\) cm.
\(SH\) est égal à \(4,5\) cm donc \(H\) est sur le cercle de centre \(S\) et de rayon \(4,5\) cm.
\(SHI\) est donc un triangle rectangle dont l’hypoténuse est le segment \([SI]\).
\([SI]\) est donc le plus grand côté, sa longueur est donc supérieure à \(4,5\) cm.
Question 6
On sait que Aire \(IJKLMNOP = 63 \) cm²
Le disque de centre \(S\) et de diamètre \(9\) cm a-t-il une aire supérieure à l'aire de loctogone ?
On connait déjà l'aire de l'octogone (cf. question 4), il suffit maintenant de calculer l'aire du disque.
Aire du disque = \( \pi \times R^2\)
Aire du disque = \( \pi \times 4,5^2\)
Aire du disque \( \approx 63,6\) cm2
Par conséquent, nous en déduisons que le disque de centre \(S\) et de diamètre \(9\) cm a bien une aire supérieure à celle de l'octogone \(IJKMNOP\).
On connait déjà l’aire de l’octogone (cf. question 4), il suffit maintenant de calculer l’aire du disque.
Aire du disque = \( \pi \times R^2\)
