L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Quelle est la nature du triangle $UVW$ ?
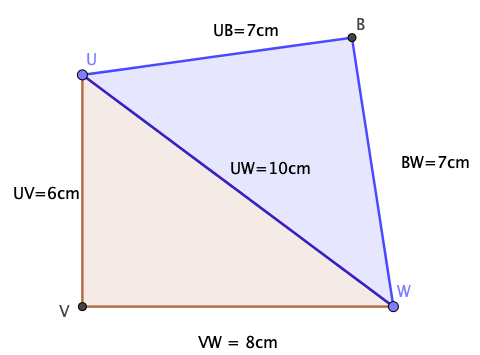
Quelconque
Isocèle
Rectangle
Rectangle et isocèle
Il faut tester la réciproque de Pythagore.
Dans le triangle $UVW$, on calcule séparément :
$UW^2=10^2=100$
De même,
$UV^2+VW^2=6^2+8^2=36+64=100$
Il apparait que $UV^2+VW^2=UW^2$ donc d'après la réciproque de Pythagore,
Le triangle est rectangle en $V$.
Question 2
Calculer l'aire de $UVW$ en $cm^2$.

$24$
$48$
$30$
$40$
Le triangle $UVW$ étant rectangle, on utilise la formule :
$A=\dfrac{Base \times hauteur}{2}$
$A=\dfrac{VW \times VU}{2}$
$A=\dfrac{8 \times 6}{2}$
$A=24$
Question 3
Quelle est la nature de $UBW$ ?

Rectangle
Isocèle rectangle
Quelconque
Isocèle
Deux côtés mesurent chacun $7$cm.
Comme $BU=BW$, le triangle est isocèle en $B$.
Est-il rectangle ?
Dans le triangle $UBW$, on calcule séparément :
$UW^2=10^2=100$
De même,
$UB^2+BW^2=7^2+7^2=49+49=98$
Il apparait que $UV^2+VW^2\neq UW^2$ donc d'après la contraposée de la propriété de Pythagore,
Le triangle n'est pas rectangle en $V$.
