Fiche de cours
Fonction linéaire, fonction affine
Fonctions linéaires
Une fonction linéaire est un procédé qui à un nombre $x$ associe un nombre $f(x)$ de la forme $f(x) = ax$ où $a$, le coefficient directeur, est un nombre donné et on la note $x \xrightarrow{f} f(x) = ax$.
Une fonction linéaire aura pour représentation graphique une droite passant toujours par l'origine du repère, c'est à dire le point de coordonnées $(0; 0)$.
Selon la valeur de $a$, l'inclinaison de la droite sera différente : plus $a$ est grand (et positif), plus la droite monte, plus $a$ est petit et positif, moins la droite monte. Si $a$ est négatif, la droite descend.
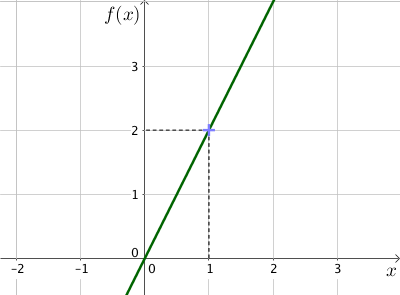
Sur le graphique, la fonction $f$ associe au nombre 1 le nombre 2.
Ainsi $f(1) = 2$.
Or la forme générale de $f$ est $f(x) = a \times x$ donc $f(1) = a \times 1
