L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle est la (ou les) solution(s) de l'équation \((2x + 1) - (x - 3) = 0\) ?
- 0,5 et 3
2
-4
-0,5
Il suffit de remplacer \(x\) par les valeurs proposées, et voir si l’égalité devient vraie.
Attention, ce n’est pas une « équation-produit ».
Commencez par supprimer toutes ces parenthèses.
Pas de problème pour les premières parenthèses. Attention les suivantes sont précédées d’un signe « - » donc vous allez devoir « inverser » tous les signes.
Question 2
Quelles sont les solutions de l'équation \((2x + 4)(x - 9) = 0\) ?
- 2 et 9
2 et - 9
6 et 9
- 2 et - 9
Attention, cette fois, il s’agit d’une « équation-produit ».
Si un produit est nul, alors l’un, au moins, des facteurs est nul.
\( 2x + 4 = 0\) ou \(x – 9 = 0\)
Question 3
Quelles sont les solutions de l'équation \((x - 5)(3x + 4) = 0\) ?
\(\dfrac{4}{3}\) et 5
\(\dfrac{4}{3}\) et - 5
\(-\dfrac{4}{3}\) et -5
\(-\dfrac{4}{3}\) et 5
Attention, cette fois, il s’agit d’une « équation-produit ».
Si un produit est nul, alors l’un, au moins, des facteurs est nul.
\( x - 5 = 0\) ou \(3x + 4 = 0\)
Question 4
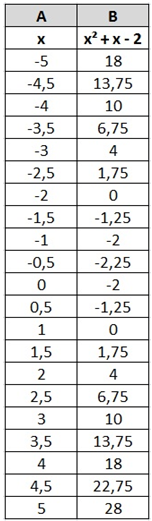
On a calculé en colonne B, les valeurs prises par l'expression \(x^2 + x - 2\) pour les valeurs de \(x\) inscrites en colonne A.
Que pouvez-vous dire sur la (les) solution(s) de l'équation \(x^2 + x - 2 = 4\) ? 
2 est l’unique solution.
-3 et 2 sont solutions.
2 est solution mais il y en a deux autres.
2 n’est pas solution.
18 est l’unique solution.
Dans la colonne B, cherchez les valeurs de \(x\) pour lesquelles \(x^2 + x – 2\) prend la valeur 4.
4 apparait deux fois dans la colonne B.
Question 5
On utilise toujours le même tableau.
De quelle équation le nombre 0 est-il solution ?
\(x^2 + x - 2 = 1\)
\(x^2 + x - 2 = 0\)
\(x^2 + x - 2 = 4\)
\(x^2 + x - 2 = -2\)
Le tableau est-il vraiment utile ?
Si \(x = 0\) alors \(x^2 + x - 2 =\) ?