Fiche de cours
I. Schéma
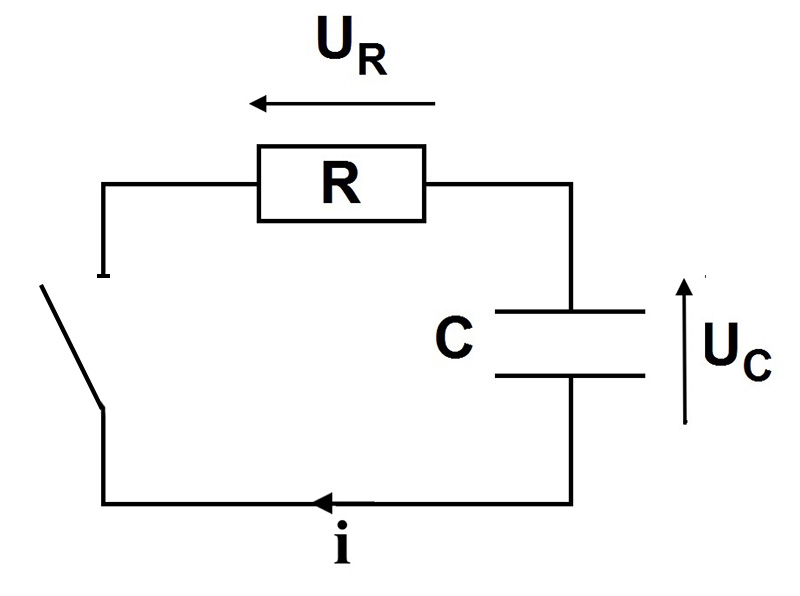
On dit que le condensateur est chargé lorsqu’à ses bornes il existe déjà une tension. Cette tension est notée $E.$
A $t = 0^-$ (juste avant $t = 0), u_c = E$.
A $t = 0,$ on ferme l’interrupteur donc le circuit.
Tant que l’interrupteur est ouvert, le courant ne peut pas circuler. Puisque le condensateur est chargé, il va alors se décharger. Comment ?
II. Loi des mailles
On a choisi de tourner dans le sens anti-horaire dans la maille. On a alors : $u_c + u_R = 0$.
Selon la loi d’Ohm : $u_R = R\times i$.
Donc $u_c + R\times i = 0$.
Dans le cas d’un condensateur : $i = C\dfrac{du_c}{dt}$.
On remplace dans l’équation : $u_c+RC\dfrac{du_c}{dt} = 0$. On a une équation différentielle.
On divise toute l’équation par RC : $\dfrac{du_c}{dt} + \dfrac{u_c}{\tau} = 0$, avec $RC = \tau$.
$\tau$ est la constante de temps ou temps caractéristique (s). (E) est une équation différentielle du premier ordre. Comment connaît-on l’unité de $\tau$ ?
$\dfrac{du_c}{dt}$ sont des volts sur des secondes donc $\dfrac
