L'énoncé
On va s'intéresser ici à l'étude très simplifiée d'un chauffage. On considère un fluide, ici de l'eau, se déplaçant au sein d'un circuit de tuyaux aux parois calorifugées entre deux échangeurs thermiques dont les parois ne sont plus calorifugées. On considère que l'apport de travail mécanique n'a lieu qu'une seule fois durant le cycle à l'aide d'un moteur au sein d'une pompe calorifugée, transmettant à l'eau un travail de $W = 100 J.$ De plus, l'apport de chaleur n'a lieu que dans les deux cavités. La cavité 1 est liée à une source de chaleur constante de température $T1 = 500 K.$
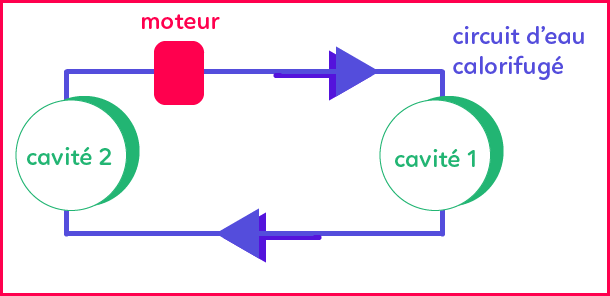
Le circuit de l'eau est décrit dans l'image ci-dessous :
Question 1
Rappeler l'expression de la variation d'énergie interne de l'eau en fonction du travail et de la chaleur dissipée dans les cas suivants :
- au sein du circuit calorifugé
- au sein des cavités
- au sein de la pompe
La formule générale est $\Delta U = W + Q.$ Nous allons donc adapter cette formule en fonction des trois niveaux du cycle :
- au sein du circuit de tuyaux calorifugés, on a $W = 0$ (pas de travail) et $Q = 0$ (pas d'échange de chaleur). Donc $\Delta U = 0.$
- au sein des cavités, on a $W = 0,$ et $Q =/= 0.$ Donc $\Delta U = Q.$
- au sein de la pompe, on a $W =/= 0$ et $Q = 0.$ Donc $\Delta U = W.$
Remarquons que $Q$ peut-être positif ou négatif.
Question 2
On considère alors que le cycle est en régime permanent, c'est-à-dire que les températures des deux cavités sont fixées et constantes au cours du temps. Nous allons nous intéresser à ces cavités ; en considérant une cavité de température $T_c,$ l'eau arrivant dans les tuyaux à une température $T_e,$ quelle est la relation liant la variation d'énergie interne au sein de la cavité, ces deux températures, et les masses et capacités thermiques de l'eau ?
On a $\Delta U = m \times c \times (T_c - T_e).$
Question 3
Si la quantité de chaleur dans la cavité 1 (chaude) est de $1000 J,$ calculer la variation de température $\Delta T$ au sein de cette cavité, en prenant comme valeurs numérique $m = 0,01 kg$ et $c = 4180 J/K/kg.$
En déduire la température de l'eau en sortie de cette cavité, si elle arrive avec une température de $300 K.$
On a $\Delta U = 1000 = m \times c \times \Delta T,$ d'où $\Delta T = \dfrac{\Delta U }{ (m \times c).}$ On obtient $\Delta T = 23,9 \approx 24 K.$
La température en sortie est alors $ T = 324 K.$
Question 4
On sait que la variation totale d'énergie interne de l'eau sur un cycle complet doit être nul (car sinon l'eau accumule infiniment de l'énergie, ce qui est impossible). En notant $Q_1$ et $Q_2$ les apports de chaleurs au sein des cavités 1 et 2, et $W$ le travail de la pompe, donner une relation liant ces trois valeurs.
En vous aidant de la question précédente, en déduire la valeur de $Q_2.$
Ceci revient à $\Delta U_{tot} = 0,$ avec $\Delta U_{tot} = W + Q_1 + Q_2.$
D'où $W + Q_1 + Q_2 = 0.$
On en déduit directement que $Q_2 = - W - Q_1 = - 100 - 1000 = - 1100 J.$
Question 5
A partir des deux questions précédentes, et en supposant que l'eau chauffée passe dans la cavité 2 à travers une eau froide sans transfert de matière (la masse de l'eau est la même que dans la cavité 1), quelle va être la température de l'eau initialement chauffée en sortie de cette seconde cavité ?
En supposant enfin que l'échange au sein de la cavité 2 est suffisamment long pour que toute la chaleur soit transférée entre les deux circuits d'eau, donner la variation de température fournie au circuit extérieur que l'on veut chauffer.
On a toujours $Q_2 = m \times c \times \Delta T,$ avec $Q_2 = - 1100 J.$
On obtient donc $\Delta T = - 26 K.$ La température en sortie de la cavité 2 est donc $324 - 26 = 298 K.$
La variation de température apportée au second circuit est de $+ 1100 J,$ puisque toute l'énergie est échangée.
Question 6
L'eau que l'on souhaite chauffer à l'extérieur est en fait sous forme solide (des glaçons par exemple). La capacité thermique de ces glaçons est de $2 060 J/K/kg,$ et que la masse de glace est $1 kg,$ calculer la variation de température apportée à cette glace pendant la durée d'un cycle.
Si l'on suppose que le glaçon est uniformément chauffé, et que sa température initiale est $253 K,$ calculer le nombre de cycles nécessaires pour faire fondre le glaçon (température finale à $273 K$).
On a $\Delta T = \dfrac{1 100 }{ (1 \times 2 060)} = 0,53 K.$
On veut une augmentation totale de $20 K$ ; on a donc $N = \dfrac{20 }{ 0,53} = 38$ cycles.
