Fiche de cours
Ensemble $\mathbb{U}$ des nombres complexes de module $1$
Définition :
On désigne par $\mathbb{U}$ l'ensemble des nombres complexes de module $1$ c'est à dire l'ensemble $\{ z \in \mathbb{C}, |z| =1 \}$.
On peut citer en guise d'exemple les nombres suivants :
- $1 \in \mathbb{U}$
- $-1 \in \mathbb{U}$
- $e^{i\frac{\pi}{2}}=i \in \mathbb{U}$
- $e^{-i\frac{\pi}{2}}=-i \in \mathbb{U}$
On pourra remarquer que $0 \notin \mathbb{U}$.
On s'intéresse à l'image de l'ensemble $\mathbb{U}$ dans le plan complexe, c'est à dire, la représentation géométrique de cet ensemble.
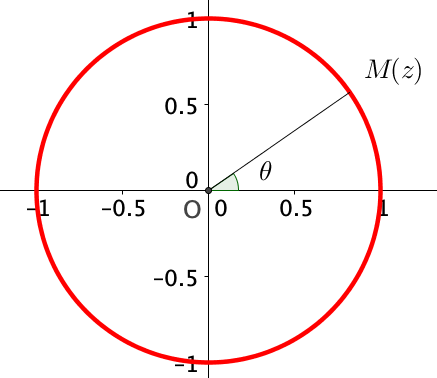
Ainsi, l'image d'un nombre complexe de module $1$ dans le plan complexe est un point du cercle trigonométrique, c'est à dire un point du cercle de rayon 1.
On dira alors que pour tout $z \in \mathbb{U}$, il existe un unique $\theta \in ]-\pi, \pi]$ tel que
$z = e^{i\theta}$.
On admet alors que l'image de $\mathbb{U}$ dans le plan complexe est le cercle trigonométrique.
Propriétés
Propriété 1 :
Soit $z \in \mathbb{
