Fiche de cours
Exercice : Image d'un nombre complexe, transformation du plan
ÉNONCÉ
On considère le plan complexe muni du repère $(O ; \vec{u} ; \vec{v})$ orthonormé direct ainsi que les points $A$ et $B$ représentés ci-dessous :
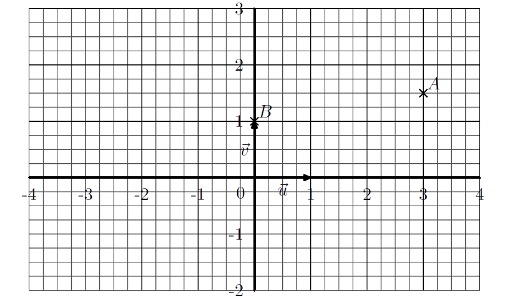
On note $z_A$ et $z_B$ les affixes respectives des points $A$ et $B.$
QUESTIONS
1. Donner les écritures algébriques des affixes des points $A$ et $B.$
2. Placer le point $C$ d’affixe $-z_A.$ Quelle transformation géométrique permet de transformer le point $A$ en $C$ ?
3. Placer le point $D$ d’affixe $\overline{z_A}.$ Quelle transformation géométrique permet de transformer le point $A$ en $D$ ?
4. Placer le point $E$ d’affixe $-\overline{z_A}.$ Quelle transformation géométrique permet de transformer le point $A$ en $E$ ?
5. Placer le point $F$ d’affixe $\frac{1}{2}.z_A.$ Que peut-on dire de la position du point $F$ ?
6. Placer le point $G$ d’affixe $z_A+(-2-2.i).$ Quelle transformation géométrique permet de transformer le point $A$ en $G$ ?
7. On considère l
