Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Raisonnement par disjonction de cas
Principe
Pour prouver qu'une proposition est vraie sur un ensemble $E$, on peut monter qu'elle est vraie sur des sous-ensembles disjoints de $E$, dont la réunion est $E$.
Le raisonnement par disjonction de cas consiste donc à séparer différents cas.
Illustration graphique
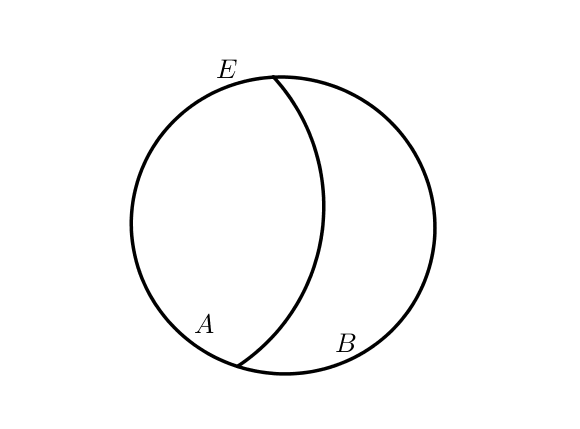
Dans l'exemple ci-dessous, les deux sous-ensembles $A$ et $B$ sont séparés et en les réunissant, on obtient la totalité de $E$.
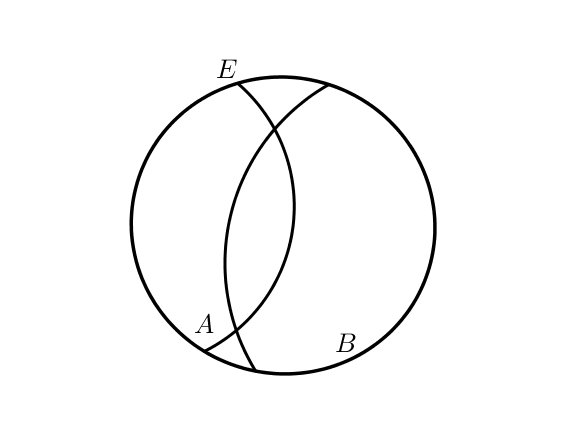
Dans ce deuxième exemple, les deux sous-ensembles ne sont pas tout à fait séparés dans la mesure où il existe une partie commune, mais la réunion est toujours égale à $E$. Dans ce cas, on ne pourrait pas raisonner par disjonction de cas.
Exemple :
On souhaite, en guise d'exemple, montrer que la propos
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
