Fiche de cours
Limites de suites
Définitions :
On dit que $(u_n)$ admet pour limite $l$ si pour $n$ suffisamment grand, les termes de la suite $(u_n)$ se rapprochent aussi proche que désiré du nombre réel $l$.
Sur le schéma, on remarque qu'au bout d'un certain rang $n$, les termes se rapprochent de $l$.
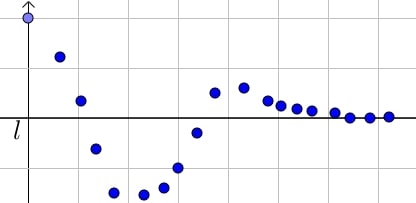
On dit alors que $(u_n)$ converge vers $l$ et on note $\lim \limits_{n \to +\infty} u_n = l$.
Si $(u_n)$ n'admet pas de limite finie ou aucune limite, alors $(u_n)$ est dite divergente.
Exemples :
$\lim \limits_{n \to +\infty} n^2 = +\infty$. La suite $u_n = n^2$ est divergente.
$\lim \limits_{n \to +\infty} \sqrt{n} = +\infty$. La suite $u_n = \sqrt{n} $ est divergente.
$\lim \limits_{n \to +\infty} \dfrac{1}{n} = 0$. La suite $u_n = \dfrac{1}{n}$ est convergente.
$\lim \limits_{n \to +\infty} 3 + \dfrac{1}{n} = 3$. La suite $u_n = 3+ \dfrac{1}{n}$ est convergente.
La suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n = (-1)^n$ prend successivement les valeurs $-1$ et $1$ selon que $n$ soit impaire ou paire.
Les valeurs de la suite ne peuvent donc pas se rapprocher dans un petit intervalle autour d'un nombre réel.
Ainsi la suite $u_n
