Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Propriétés analytiques
La fonction $\ln $ est définie et dérivable sur $]0;+\infty[$.
Pour tout réel $\displaystyle x>0, (\ln x)'= \dfrac{1}{x}$.
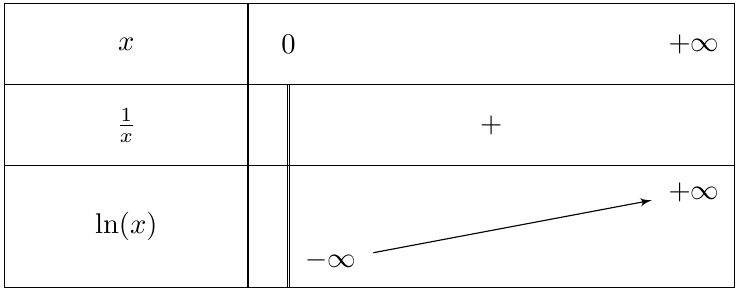
La fonction $\ln $ est continue et strictement croissante sur $]0;+\infty[$.
D'autre part,
$\ln (1)=0$
$\ln (e)=1$
$\displaystyle\lim\limits_{x \rightarrow +\infty} \ln x= +\infty$
$\displaystyle \lim_{\substack{x \to 0\\ x > 0}} \ln x=-\infty$
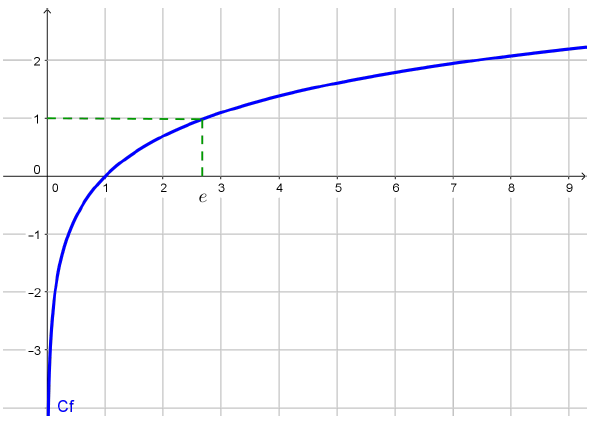
Variations et représentation graphique