L'énoncé
Soit \(f\) une fonction définie et continue sur \(I = [-4;1]\).
\(f(x)= x^3 + 6x^2 +9x +3\)
Le tableau de variations de $f$ est le suivant : 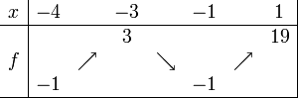
On admettra que les variations représentées sont strictes, c'est-à-dire que la fonction est soit strictement croissante, soit strictement décroissante sur les intervalles représentés.
Question 1
En justifiant votre réponse, déterminer le nombre de solutions de l'équation \(f(x) = 2\) dans \(I\).
\(f\) est continue et strictement croissante sur $[-4 ; -3]$, à valeurs dans $[-1 ; 3]$ contenant $2$.
Donc, d'après le théorème des valeurs intermédiaires pour les fonctions strictement monotones, l'équation \(f(x) = 2\) admet une solution unique dans $[-4 ; -3]$ ;
\(f\) est continue et strictement décroissante sur $[-3 ; 1]$, donc le même théorème assure que l'équation \(f(x) = 2\) admet aussi une solution unique sur $[-3 ; 1]$ ;
\(f\) est continue et strictement croissante sur $[-1 ; 1]$, à valeurs dans $[-1 ; 19]$ qui contient $2$ donc, d'après le même théorème, l'équation \(f(x) = 2\) admet une solution unique dans $[-1 ; 1]$.
Conclusion : L'équation \(f(x) = 2\) admet exactement $3$ solutions dans $[-4 : 1]$.
Remarque générale sur la question : Une première idée est d’essayer avant toute chose de faire un schéma à main levée de ce à quoi pourrait ressembler la fonction. Bien entendu, il faut être conscient qu’un tableau de variation comme celui-ci ne permet pas de déterminer le tracé exact de la fonction \(f\).
Remarquer que la fonction \(f\) qui est une fonction polynôme est continue sur \(\mathrm{R}\).
Utiliser le corollaire du TVI en justifiant correctement que l’on est sur un intervalle où la fonction est continue et strictement monotone.
Attention, il faut peut-être considérer séparément des sous intervalles de \([-4,1]\) pour qu’elle soit strictement monotone.
Question 2
Justifier que l'équation \(f(x) = 4\) admet une solution unique, \(\alpha\), dans l'intervalle \(I\).
Nombre de solutions de l'équation \(f(x) = 4 \)
\(f\) admet en $-3$ un maximum égal à $3$ sur l'intervalle $[-4 ; -1]$ donc $4$ n'a pas d'antécédent dans cet intervalle, l'équation \(f(x) = 4\) n'admet donc pas de solution sur $[-4 ; -1]$.
Sur [-1 ; 1], \(f\) est continue et strictement croissante et prend ses valeurs dans [-1 ; 19].
Or, $4 \in [-1 ; 19]$. Donc, d'après le théorème des valeurs intermédiaires pour les fonctions continues et strictement monotones, l'équation \(f(x) = 4\) admet une solution unique dans $[-1 ; 1]$.
Conclusion : L'équation \(f(x) = 4\) admet une solution unique \(\alpha\) dans $[-4 ; 1]$.
Pour justifier l’existence de cette solution il faut à nouveau appliquer le corollaire du TVI pour les fonctions continues et monotones dans un sous-intervalle de \([-4,1]\) à définir.
Ne pas oublier de prouver l’unicité, pour cela on montrera que $4$ n’a pas d’antécédent dans les autres sous-intervalles de \([-4,1]\).
Question 3
Déterminer un encadrement de \(\alpha\) entre deux entiers consécutifs (en justifiant votre réponse).
D'après la question précédente, \(\alpha \in [-1 ; 1]\), c'est-à-dire \(-1 \leq \alpha \leq 1\) .
Or, on souhaite un encadrement plus précis de \(\alpha\) entre deux entiers consécutifs. On remarque que :
\(f(0) = 3\) et que \(f(1) = 19\) donc \(f(0) < 4 < f(1)\)
Par stricte croissance de \(f\) il vient : \( 0<\alpha<1\)
Conclusion : \(\alpha \in]0 ; 1[\) (encadrement de \(\alpha\) par deux entiers consécutifs)
Dans cette question, on s’intéresse à la solution précédente de \(f(x)=4\). On a trouvé un intervalle dans lequel est contenu \(\alpha\).
Si tu ne l’a pas trouvé au a., voici l’intervalle I cela va te servir pour cette question !!
\(I=[-1,1]\)
Rappel : Deux entiers consécutifs sont deux entiers qui se suivent. Ex : 2 et 3, 7 et 8, 67 et 68. Par contre 5 et 8 ne sont pas consécutifs.
Il faut donc tester les images d’entiers consécutifs, et en trouver deux dont les images encadrent 4. Faire un schéma.
Question 4
Déterminer une valeur approchée par excès de \(\alpha\) au millième près (en justifiant votre réponse).
Pour trouver une valeur approchée au millième de \(\alpha\) on utilise la table de valeur de la calculatrice et la méthode du balayage.
On commence avec un pas égal à $0,1$ (au dixième) en traçant la table à partir de $0$ .
On obtient facilement \(f(0,1) =3,961\) et \(f(0,2)=5,048\) donc \(0,1< \alpha <0,2\).
On recommence avec une table qui débute en $0,1$ avec un pas de $0,01$ (on va s'approcher au centième de \(\alpha\)).
On trouve facilement : \(f(0,1) =3,961\) et \(f(0,11) \approx 4,064\) donc par stricte croissance de \(f\) : \(0,1< \alpha <0,11\).
Enfin, l'encadrement au millième va être obtenu par lecture de la table commençant en $0,1$ avec un pas de $0,001$ :
\(f(0,103) \approx 3,992\) et \(f(0,104)=4,002\) donc par stricte croissance de \(f\) : \( 0,103< \alpha <0,104\).
Une valeur approchée par excès de \(\alpha\) au millième près est: $0,104$.
Une telle question nécessite une relecture des questions précédentes. Les réponses précédemment données permettent d’énoncer un résultat. Lequel ?
Question 5
On admet que l'équation \(f(x) = 0\) admet une solution unique \(\beta\) dans \([-3 ; -1]\).
Déterminer un encadrement de \(\beta\) à \(10^{-2}\) près (en justifiant la réponse).
De même pour un encadrement de \(\beta\) :
On trace la table partant de $-3$ avec un pas de $1$.
On remarque que \(\beta\) se trouve entre $-2$ et $-1$ donc on va donc pouvoir réduire l'intervalle de départ.
On retrace une nouvelle table partant de $-2$ avec un pas de $0,1$.
On en déduit que : \(-1,7 < \beta< -1,6\) .
On trace donc une dernière table partant de $-1,7$ avec un pas de $0,01$, on en déduit l'encadrement demandé10\(^{-2}\) près :
\(-1,66< \beta <-1,65 \)
C'est la même méthode qu'aux questions précédentes.
