Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Propriétés analytiques
La fonction $e^x$ est définie et dérivable sur $\mathbb{R}$.
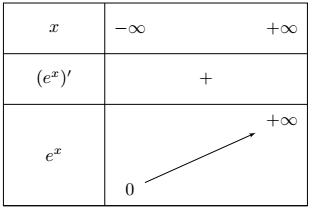
Pour tout réel $x$, $(e^x)'= e^x$ et $e^0=1$:
On a aussi :
$e^x>0$
$\lim \limits_{x \rightarrow -\infty} e^x=0$
$\lim \limits_{x \rightarrow +\infty} e^x= +\infty$
$e^1 =e \approx 2,71$
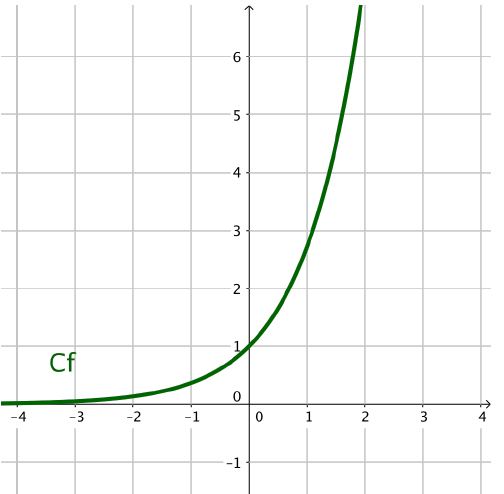
La fonction exponentielle a une dérivée strictement positive donc elle est strictement croissante sur $\mathbb{R}$.
Représentation graphique de la fonction exponentielle