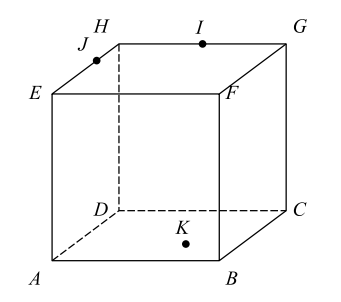
$ABCDEFGH$ est un cube. $I$ et $J$ sont deux points des arêtes $[GH]$ et $[EH]$, et $K$ est dans le plan $(BCD)$.
1) Reproduire ou imprimer la figure.
2) Construire l’intersection des plans $(ABC)$ et $(IJK)$. Justifier la construction.
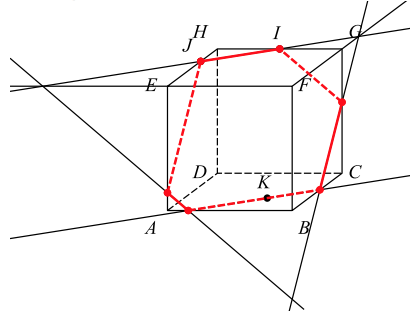
3) Tracer la section du cube par le plan $(IJK)$.
2) Les points $I$ et $J$ appartiennent aux plans $(EFG)$ et $(IJK)$, donc la droite $(IJ)$ est l’intersection des plans $(EFG)$ et $(IJK)$.
De plus, comme $ABCDEFGH$ est un cube, les plans $(ABC)$ et $(EFG)$ sont parallèles donc le plan $(IJK)$ coupe ces deux plans en formant deux droites parallèles.
La droite d’intersection des plans $(IJK)$ et $(ABC)$ est donc la parallèle à $(IJ)$ passant par $K$.
3) Voir figure.