Le but de cet exercice est d’examiner, dans différents cas, si les hauteurs d’un tétraèdre sont concourantes, c’est-à-dire d’étudier l’existence d’un point d’intersection de ses quatre hauteurs. On rappelle que dans un tétraèdre $MNPQ$, la hauteur issue de $M$ est la droite passant par $M$ orthogonale au plan ($NPQ$).

Partie A

Étude de cas particuliers On considère un cube $ABCDEFGH$.

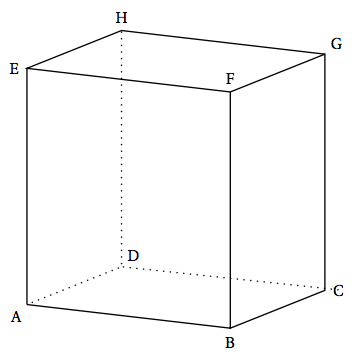
On admet que les droites $(AG), (BH), (CE)$ et $(DF)$, appelées « grandes diagonales » du cube, sont concourantes.

1. On considère le tétraèdre $ABCE$.

   a. Préciser la hauteur issue de $E$ et la hauteur issue de $C$ dans ce tétraèdre.

   b. Les quatre hauteurs du tétraèdre $ABCE$ sont-elles concourantes ?

2. On considère le tétraèdre $ACHF$ et on travaille dans le repère  $(A ;\vec{AB};\vec{AD};\vec{AE})$ .

   a. Vérifier qu’une équation cartésienne du plan $(ACH)$ est : $x − y + z = 0$.

   b. En déduire que $(FD)$ est la hauteur issue de $F$ du tétraèdre $ACHF$.

   c. Par analogie avec le résultat précédent, préciser les hauteurs du tétraèdre $ACHF$ issues respectivement des sommets $A, C$ et $H$. Les quatre hauteurs du tétraèdre $ACHF$ sont-elles concourantes ?

Dans la suite de cet exercice, un tétraèdre dont les quatre hauteurs sont concourantes sera appelé un tétraèdre orthocentrique.

Partie B

Une propriété des tétraèdres orthocentriques Dans cette partie, on considère un tétraèdre $MNPQ$ dont les hauteurs issues des sommets $M$ et $N$ sont sécantes en un point $K$. Les droites $(MK$) et ($NK$) sont donc orthogonales aux plans ($NPQ$) et ($MPQ$) respectivement.

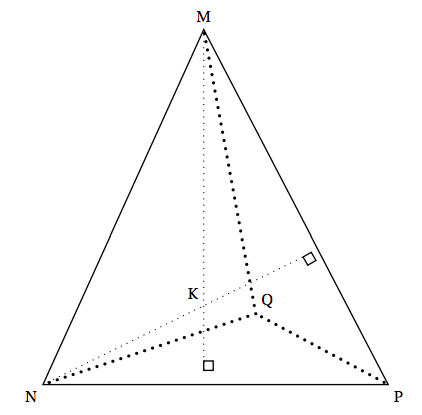
1. a. Justifier que la droite (PQ) est orthogonale à la droite (MK); on admet de même que les droites (PQ) et (NK) sont orthogonales.

    b. Que peut-on déduire de la question précédente relativement à la droite (PQ) et au plan (MNK) ? Justifier la réponse.

2. Montrer que les arêtes [MN] et [PQ] sont orthogonales.

Ainsi, on obtient la propriété suivante : Si un tétraèdre est orthocentrique, alors ses arêtes opposées sont orthogonales deux à deux. (On dit que deux arêtes d’un tétraèdre sont « opposées » lorsqu’elles n’ont pas de sommet commun.)

Partie C

Application : dans un repère orthonormé, on considère les points : $R(−3 ; 5 ; 2),S(1 ; 4 ; −2),T(4 ; −1 ; 5)$ et $U(4 ; 7 ; 3)$.

Le tétraèdre $RSTU$ est-il orthocentrique ? Justifier.