L'énoncé
On considère plusieurs sacs de billes \(S_1\), \(S_2\), ..., \(S_n\), ... tels que :
– le premier, \(S_1\), contient 3 billes jaunes et 2 vertes ;
– chacun des suivants, \(S_2\), \(S_3\), ..., \(S_n\), ... contient 2 billes jaunes et 2 vertes.
Le but de cet exercice est d’étudier l’évolution des tirages successifs d’une bille de ces sacs, effectués de la manière suivante :
– on tire au hasard une bille dans \(S_1\);
– on place la bille tirée de \(S_1\) dans \(S_2\), puis on tire au hasard une bille dans \(S_2\);
– on place la bille tirée de \(S_2\) dans \(S_3\), puis on tire au hasard une bille dans \(S_3\);
– etc.
Pour tout entier \(n \geq 1\), on note \(E_n\) l’évènement : «la bille tirée dans \(S_n\) est verte» et on note \(P(E_n)\) sa probabilité.
Question 1
D'après l'énoncé, donner les valeurs de \(P(E_1)\), \(P_{E_1}(E_2)\), \(P_\overline{{E_1}}(E_2)\).
En déduire la valeur de \(P(E_2)\).
\(S_1\) contient 3 billes jaunes et 2 vertes. On note : \(E_1\): «la bille tirée dans \(S_1\) est verte» donc \(P(E_1)=\dfrac{2}{5}\).
\(S_2\) contient 2 billes jaunes et 3 vertes. Sachant qu'on a tiré une bille verte dans \(S_1\) et qu'on la placée dans \(S_2\),
La probabilité de tirer une bille verte est :
\(P_{E_1}(E_2)=\dfrac{3}{5}\)
De même : \(P_{\overline{E_1}}(E_2)=\dfrac{2}{5}\).
On cherche la probabilité d'un seul événement, la question commence par en déduire. \(E_1\) et \(\overline{E_1}\) forment une partition de l'univers, d'après la formule de probabilité totale :
\(P(E_2)= P(E_2 \cap E_1)+P(E_2 \cap \overline{E_1})\)
\(P(E_2)=P_{E_1}(E_2)\times P(E_1)+P_{\overline{E_1}}(E_2)\times P(\overline{E_1})\)
\(P(E_2)=\dfrac{3}{5}\times \dfrac{2}{5}+\dfrac{2}{5}\times\dfrac{3}{5}\)
\(P(E_2)=0,48\)
Connaissez-vous les probabilités conditionnelles ? Un doute ? Regardez la vidéo.
Quel est l’évènement contraire de \(E_1\) ?
Pour trouver \(P(E_2)\), il faut utiliser la formule de probabilité totale :
\(P(E_2)= P(E_2 \cap E_1) + P(E_2 \cap \overline{E_1})\).
Question 2
À l'aide d'un arbre pondéré, exprimer \(P(E_{n+1})\) en fonction de \(P(E_n)\).
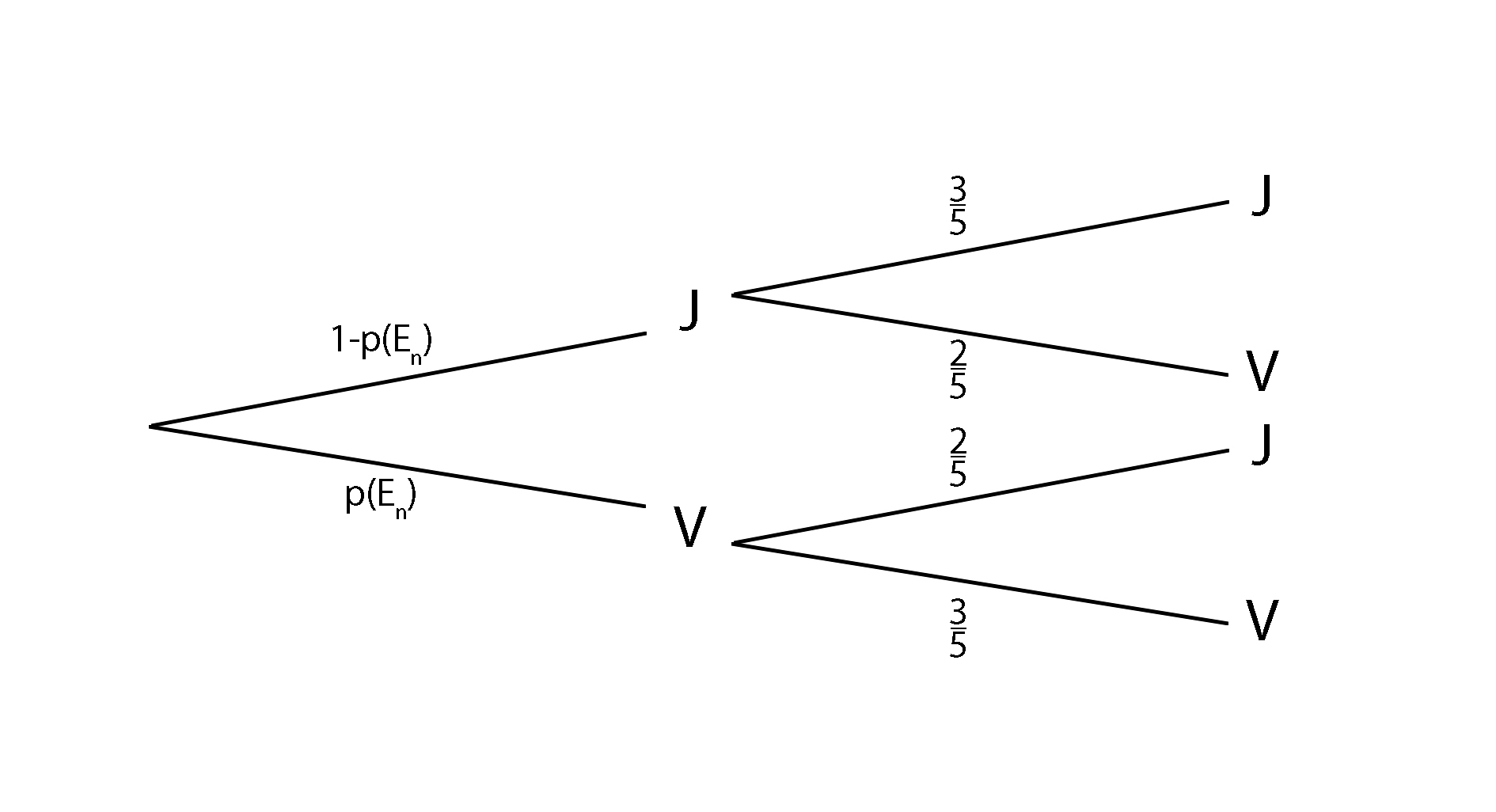
On cherche la probabilité d'un seul événement, \(E_n\) et \(\overline{E_n}\) forment une partition de l'univers, d'après la formule des probabilités totales :
\(P(E_{n+1})=P(E_{n+1} \cap E_n)+P(E_{n+1} \cap \overline{E_n})\)
\(P(E_{n+1})=P_{E_n}(E_{n+1})\times P(E_n)+P_{\overline{E_n}}(E_{n+1})\times P(\overline{E_n})\)
\(P(E_{n+1})=\dfrac{3}{5}\times P(E_n)+\dfrac{2}{5}\times (1-P(E_n))\)
\(P(E_{n+1})=\dfrac{1}{5}\times P(E_n)+\dfrac{2}{5}\)
Utilisez la formule des probabilités totales avec \(E_{n+1}\) et \(E_n\).
Question 3
Étude dune suite
On considère la suite \((u_n)\) définie par :
\(\left\{\begin{array}{left}u_1 = \dfrac{2}{5} \\ u_{n+1} = \dfrac{1}{5} u_n +\dfrac{2}{5} \, pour \, tout \, n \geq 1 \end{array}\right.\)
Démontrer que la suite \((u_n)\) est majorée par \(\dfrac{1}{2}.\)
Montrons que la suite \((u_n)\) est majorée par \(\dfrac{1}{2}\), c'est à dire que \(u_n \leq \dfrac{1}{2}\)
On va utiliser le raisonnement par récurrence.
- Initialisation : \(u_1=\dfrac{2}{5}\leq \dfrac{1}{2}\)
La propriété est vraie pour \(n=1\)
- Hérédité : Supposons que pour un certain rang \(n\), \(u_n \leq\dfrac{1}{2}\)
Montrons que \(u_{n +1} \leq \dfrac{1}{2}\)
\(u_{n+1}=\dfrac{1}{5}u_n+\dfrac{2}{5}\)
D'après l'hypothèse de récurrence, \(u_n\leq\dfrac{1}{2}\)
Donc \(\dfrac{1}{5}u_n\leq\dfrac{1}{5}\times \dfrac{1}{2}\)
\(\dfrac{1}{5}u_n+\dfrac{2}{5}\leq\dfrac{1}{10}+\dfrac{2}{5}=\dfrac{5}{10}=\dfrac{1}{2}\)
Donc \(u_{n+1}\leq\dfrac{1}{2}\)
Conclusion, pour tout \(n \geq 1\), \(u_n\leq\dfrac{1}{2}\)
Avez-vous pensé à utiliser une démonstration par récurrence ? Un doute ? Regardez la vidéo sur les démonstrations par récurrence.
Question 4
Démontrer que \((u_n)\) est croissante.
Montrons que la suite \((u_n)\) est croissante, c'est à dire, montrons que \(u_{n+1}-u_n \geq 0\).
\(u_{n+1}-u_n = \dfrac{1}{5}u_n + \dfrac{2}{5}-u_n \)
\(u_{n+1}-u_n= -\dfrac{4}{5}u_n+\dfrac{2}{5}\)
On sait que \(u_n<\dfrac{1}{2}\) donc
\(-\dfrac{4}{5}u_n>-\dfrac{4}{5}\times \dfrac{1}{2}=-\dfrac{2}{5} \)
\( -\dfrac{4}{5}u_n+\dfrac{2}{5}\geq 0\)
\( u_{n+1}-u_n \geq 0\)
Donc la suite \((u_n)\) est croissante.
Pour montrer qu’une suite est croissante, on calcule \(u_{n+1} – u_n\).
Question 5
Justifier que la suite \((u_n)\) est convergente et préciser sa limite.
La suite \((u_n)\) est croissante et majorée par \(\dfrac{1}{2}\) donc la suite est convergente et converge vers un certain nombre \(l\) à déterminer.
Calcul de l : \(u_{n+1}=\dfrac{1}{5}u_n+\dfrac{2}{5}\)
En passant à la limite, \(l\) vérifie :
\(l=\dfrac{1}{5}l+\dfrac{2}{5} \Leftrightarrow 5l=l+2 \Leftrightarrow l=\dfrac{1}{2}\)
Une suite croissante et majorée est convergente ! Relisez votre cours sur les suites si vous ne vous en souveniez plus.
\(u_{n+1} = \dfrac{1}{5} u_n + \dfrac{2}{5}\)
Il suffit ensuite de passer à la limite.
Question 6
Sachant que \(P(E_n) = u_n\) et à l'aide des résultats précédents, déterminer l'évolution des probabilités \(P(E_n)\).
Evolution des probabilités \(P(E_n)\) avec \(P(E_n) = u_n\)
On parle d'évolution donc \(n\) est grand.
\(\lim\limits_{n \to +\infty}u_n=\dfrac{1}{2}\) donc
\(P(E_n) \underset{n\to+\infty}{\longrightarrow} \dfrac{1}{2}\)
Apres un grand nombre de tirages, il y a une chance sur deux de tirer une bille verte.
D’après la question précédente, l’évolution de \(P(E_n)\) est la même que celle de \(u_n\).
Question 7
Montrer que la suite $V$ définie par : \(V_n = u_n -0,5\) est une suite géométrique.
\(V_{n+1}=u_{n+1}-\dfrac{1}{2}\)
\(V_{n+1}=\dfrac{1}{5}u_n+\dfrac{2}{5}-\dfrac{1}{2}\)
\(V_{n+1}=\dfrac{1}{5}u_n-\dfrac{1}{10}\)
\(V_{n+1}=\dfrac{1}{5}(u_n-\dfrac{1}{2})\)
\(V_{n+1}=\dfrac{1}{5}V_n\)
Donc \(V_n\) est une suite géométrique de raison \(q=\dfrac{1}{5}\) et de premier terme :
\(V_1 = u_1-\dfrac{1}{2}= \dfrac{2}{5}-\dfrac{1}{2} = -\dfrac{1}{10}\)
Donc \(V_n=-\dfrac{1}{10}\left(\dfrac{1}{5}\right)^{n-1}\)
Un doute sur les suites géométriques ? Regardez la vidéo.
Question 8
Déterminer la plus petite valeur de \(n\) pour laquelle on a : \(0,499 99 \leq P(E_n) \leq 0,5\)
On cherche \(n\) tel que :
\(0,49999 \leq u_n \leq 0,5\)
\( \Leftrightarrow 0,49999-0,5 \leq u_n-0,5 \leq 0,5-0,5\)
\( \Leftrightarrow -10^{-5} \leq V_n \leq 0\)
\(\Leftrightarrow -10^{-5} \leq -\dfrac{1}{10}\left(\dfrac{1}{5}\right)^{n-1}\)
\( \Leftrightarrow 10^{-4} \geq \dfrac{1}{5^{n-1}}\)
\( \Leftrightarrow 5^{n-1}\geq10^4\)
\( \Leftrightarrow \ln(5^{n-1}) \geq \ln(10^4)\)
\( \Leftrightarrow (n-1)\ln(5) \geq 4\ln(10)\)
\(n \geq 4\dfrac{\ln(10)}{\ln(5)}+1\approx 6,8\)
Il faut donc prendre \(n = 7\).
Avez-vous pensé à utiliser les logarithmes pour trouver la valeur de \(n\) correspondante ?
